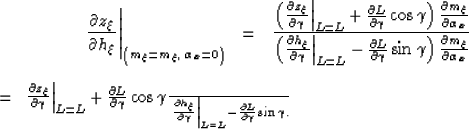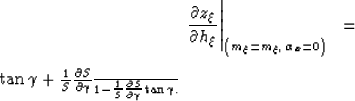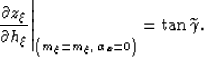Next: Numerical examples of aperture
Up: Kinematic analysis of ADCIGs
Previous: Generalized migration impulse response
The expression for the generalized impulse response
of prestack anisotropic migration leads to the analytical
evaluation of the offset dip and midpoint
dip along the planes tangent to the impulse response,
as a function of the group angles and velocity.
In this section I demonstrate that in the simple case
of flat reflectors this analysis leads to exactly the
same results as the phase-space analysis presented in the previous section.
The derivation of the general relationships expressed
in equations 13 and 12,
which are valid for an arbitrary reflector's dip,
is left to the reader.
By applying elementary analytical geometry,
I demonstrate in Appendix A that
the derivative of the depth with respect to the subsurface offset,
at constant midpoint, is given by:
| 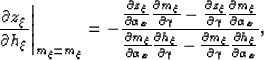 |
(25) |
and the derivative of the depth with respect to the midpoint,
at constant subsurface offset, is given by:
| 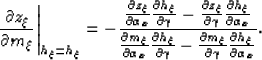 |
(26) |
In the special case of flat reflectors the
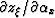 and
and
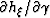 vanish,
and thus equation 25 simplifies into
the following expression:
vanish,
and thus equation 25 simplifies into
the following expression:
| 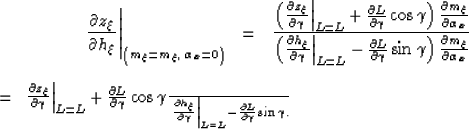 |
|
| (27) |
By substituting into equation 27
the appropriate derivative of the image coordinates
and of the half path-length
with respect to the angles,
all provided in Appendix A,
I further simplify the expression into the following:
| 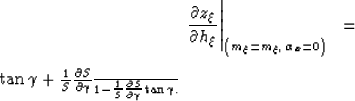 |
(28) |
Finally, by applying the transformation
from group angles into phase angles expressed
in equation 4,
I obtain the final result that for flat reflectors
the subsurface-offset dip is exactly equal to
the tangent of the phase aperture angle 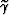 ;that is:
;that is:
| 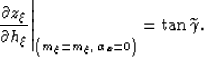 |
(29) |





Next: Numerical examples of aperture
Up: Kinematic analysis of ADCIGs
Previous: Generalized migration impulse response
Stanford Exploration Project
5/3/2005
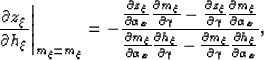
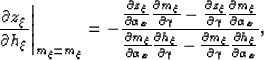
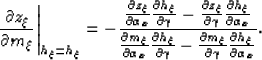
![]() and
and
![]() vanish,
and thus equation 25 simplifies into
the following expression:
vanish,
and thus equation 25 simplifies into
the following expression: