BACKGROUND

Estimation of a stationary PEF can be phrased as a least-squares problem, where the following fitting goal is minimized with respect to an unknown filter f:  

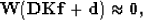$$\bold{W(DKf + d)} \approx \bold 0 ,$$ (1)

in which W is a weight to exclude equations with missing data, D is convolution with the data, K constrains the first filter coefficient to 1, f is the unknown filter, and d is a copy of the data.

Once the PEF has been estimated, it can then be used to interpolate missing data by solving another inverse problem:  

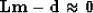$$\bold{Lm-d} \approx \bold 0$$ (2)

 

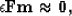$$\epsilon \bold{Fm} \approx \bold 0 ,$$ (3)

where L is a selecting operator that selects the known data within the interpolated model m, d is the known data, $\epsilon$ is a scaling factor, and F represents convolution with the newly-found PEF. The output model m is referred to as the restored data.

Instead of a restored version of the data, multiple equiprobable realizations Clapp (2000) of the missing data can be generated by changing fitting goal (3) to  

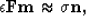$$\epsilon \bold{Fm} \approx \sigma \bold n ,$$ (4)

where instead of desiring the output of the filter convolved with the model to be zero, we now choose for it to be equal to random noise n scaled by a factor $\sigma$. Multiple realizations of the interpolation can be generated by using different random numbers for n that are identically distributed. This noise is only introduced where the data are missing, as the residual of fitting goal (3) will already look like random noise where data are present.

In geostatistical language, the restored data is very similar to an E-type, which is the same as an average of multiple realizations (or simulations) of the result generated by fitting goals (2) and (4). Dividing random noise by the PEF, which is the same as solving fitting goal (4) is equivalent to an unconditional simulation, where no data constrain the output.

All of the previous theory has been utilized for stationary PEFs. A non-stationary PEF can be estimated by a fitting goal similar to fitting goal (1), except that instead of the PEF having a single set of coefficients, the PEF now has a separate set of coefficients for each data point. Since there are now many more unknown filter coefficients than known data, a regularization term needs to be added to constrain the problem:  

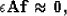$$\epsilon \bold{Af} \approx \bold 0 ,$$ (5)

where f is the unknown non-stationary PEF and A is a regularization operator that acts over space for each filter coefficient independently, and is typically either a Laplacian or helix derivative Claerbout (1999). Fitting goals (3) and (4) can be used with a non-stationary PEF f in the place of a stationary PEF.