




Next: Sensitivity kernels examples
Up: WEMVA sensitivity kernels
Previous: WEMVA sensitivity kernels
Consider a (nonlinear) function 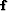 mapping
one element of the functional model space
mapping
one element of the functional model space  to
one element of the functional data space
to
one element of the functional data space 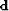 :
:
| 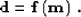 |
(70) |
The tangent linear application to 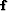 at point
at point 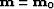 is
a linear operator
is
a linear operator 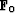 defined by the expansion
defined by the expansion
| 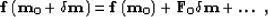 |
(71) |
where 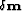 is a small perturbation in the model space.
The tangent linear application
is a small perturbation in the model space.
The tangent linear application 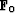 is also known under
the name of Fréchet derivative of
is also known under
the name of Fréchet derivative of 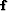 at point
at point 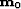 (109).
fat3.sC
(109).
fat3.sC
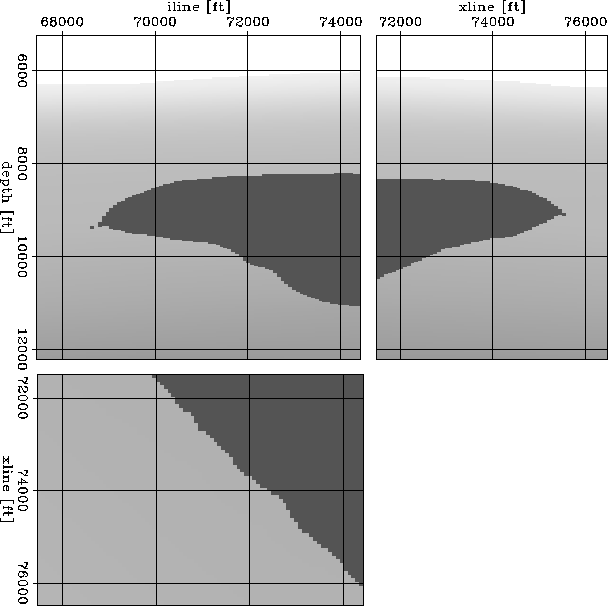
Figure 12 3D slowness model.




 fat3.fp3
fat3.fp3
Figure 13 3D sensitivity kernels for wave-equation MVA.
The frequency range is 1-16 Hz.
The kernels are complicated by the multipathing
occurring as waves propagate through the rough
salt body.
The image perturbation corresponds to a kinematic shift.




 fat3.fq3
fat3.fq3
Figure 14 3D sensitivity kernels for wave-equation MVA.
The frequency range is 1-16 Hz.
The kernels are complicated by the multipathing
occurring as waves propagate through the rough
salt body.
The image perturbation corresponds to an amplitude scaling.




 fat3.svty
fat3.svty
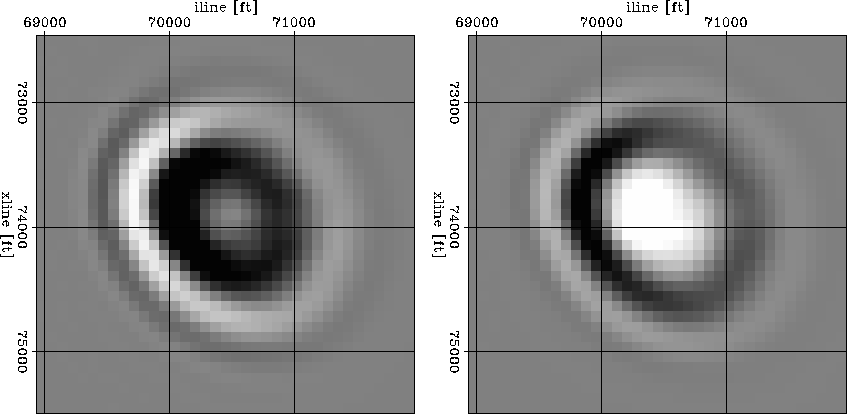
Figure 15 Cross-section of 3D sensitivity kernels for wave-equation MVA.
The left panel corresponds to an image perturbation
produced a kinematic shift, while the right panel
corresponds to an image perturbation produced by
amplitude scaling.
The lowest sensitivity occurs in the center of the
kinematic kernel (left). In contrast, the maximum
sensitivity occurs in the center of the kernel (right).





frechet.exp can be written formally as
| 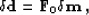 |
(72) |
where
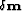 is a perturbation in the model space, and
is a perturbation in the model space, and
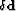 is a perturbation in the image space.
If we denote by
is a perturbation in the image space.
If we denote by 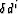 the ith component of
the ith component of 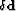 ,
and by
,
and by 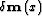 an infinitesimal element of
an infinitesimal element of 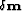 at location
at location  , we can write
, we can write
| 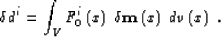 |
(73) |
F0i is, by definition, the integral kernel
of the Fréchet derivative 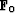 ,V is the volume under investigation,
dv is a volume element of V and
,V is the volume under investigation,
dv is a volume element of V and  is the
integration variable over V.
The sensitivity kernel, a.k.a. Fréchet derivative kernel ,
F0i expresses the sensitivity of
is the
integration variable over V.
The sensitivity kernel, a.k.a. Fréchet derivative kernel ,
F0i expresses the sensitivity of
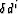 to a perturbation of
to a perturbation of 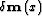 for
an arbitrary location
for
an arbitrary location  in the volume V.
in the volume V.
Sensitivity kernels occur in every inverse problem and have different meanings
depending of the physical quantities involved:
For wideband traveltime tomography
(104; 14; 3; 33; 55),
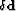 is represented by traveltime differences
between recorded and computed traveltimes in a reference medium.
The sensitivity kernels are infinitely-thin rays
computed by ray tracing in the background medium.
For finite-frequency traveltime tomography
(28; 52; 58; 76),
is represented by traveltime differences
between recorded and computed traveltimes in a reference medium.
The sensitivity kernels are infinitely-thin rays
computed by ray tracing in the background medium.
For finite-frequency traveltime tomography
(28; 52; 58; 76),
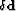 is represented by time shifts
measured by crosscorelation between the recorded wavefield
and a wavefield computed in a reference medium.
The sensitivity kernels are represented by hollow fat rays
(a.k.a. ``banana-doughnuts'') which depend on the background medium.
For wave-equation tomography
(114; 72; 73),
is represented by time shifts
measured by crosscorelation between the recorded wavefield
and a wavefield computed in a reference medium.
The sensitivity kernels are represented by hollow fat rays
(a.k.a. ``banana-doughnuts'') which depend on the background medium.
For wave-equation tomography
(114; 72; 73),
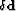 is represented by perturbations
between the recorded wavefield and the computed wavefield
in a reference medium.
The sensitivity kernels are represented by fat rays with similar forms
for either the Born or Rytov approximation.
For wave-equation migration velocity analysis
(10; 88; 89; 93),
is represented by perturbations
between the recorded wavefield and the computed wavefield
in a reference medium.
The sensitivity kernels are represented by fat rays with similar forms
for either the Born or Rytov approximation.
For wave-equation migration velocity analysis
(10; 88; 89; 93),
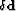 is represented by image perturbations.
The sensitivity kernels are discussed in the following sections.
is represented by image perturbations.
The sensitivity kernels are discussed in the following sections.
Wave-equation migration velocity analysis (WEMVA)
establishes a linear relation between
perturbations of the slowness model 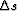 and
perturbations of migrated images
and
perturbations of migrated images 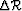 .
.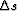 and
and 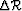 correspond, respectively, to
correspond, respectively, to 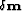 and
and 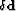 in linear.
in linear.
Formally, we can write
| 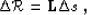 |
(74) |
where 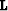 is the linear first-order Born
wave-equation MVA operator.
The operator
is the linear first-order Born
wave-equation MVA operator.
The operator 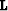 incorporates all first-order scattering
and extrapolation effects for media of arbitrary complexity.
The major difference between WEMVA and
wave-equation tomography is that
incorporates all first-order scattering
and extrapolation effects for media of arbitrary complexity.
The major difference between WEMVA and
wave-equation tomography is that 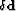 is formulated
in the image space for the former as opposed to the
data space for the later. Thus, with WEMVA we are able
to exploit the power of residual migration in perturbing
migrated images - a goal which is much harder to achieve
in the space of the recorded data.
is formulated
in the image space for the former as opposed to the
data space for the later. Thus, with WEMVA we are able
to exploit the power of residual migration in perturbing
migrated images - a goal which is much harder to achieve
in the space of the recorded data.
By construction, the linear operator 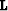 depends on
the wavefield computed by extrapolation of the surface
data using the background slowness,
which corresponds to
depends on
the wavefield computed by extrapolation of the surface
data using the background slowness,
which corresponds to 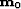 in frechet.exp.
Thus, the operator
in frechet.exp.
Thus, the operator 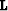 depends directly on the type of
recorded data and its frequency content,
and it also depends on the background slowness model.
Thus, the main elements that control the shape
of the sensitivity kernels are
depends directly on the type of
recorded data and its frequency content,
and it also depends on the background slowness model.
Thus, the main elements that control the shape
of the sensitivity kernels are
the frequency content of the background wavefield,
the type of source from which we generate the background
wavefield (e.g. point source, plane wave), and
the type of perturbation introduced in the image space,
which for this problem corresponds to the data space.
In the next examples, I define two types of image perturbations:
a purely kinematic type 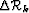 , implemented simply as a derivative
of the image with respect to depth, which can be implemented as
a multiplication in the depth domain as follows:
, implemented simply as a derivative
of the image with respect to depth, which can be implemented as
a multiplication in the depth domain as follows:
| 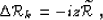 |
(75) |
and a purely dynamic type 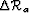 , implemented by
scaling the reference image
, implemented by
scaling the reference image 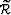 with
an arbitrary number:
with
an arbitrary number:
| 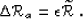 |
(76) |
In both cases, the perturbations are limited to
a small portion of the image.
The main difference between 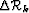 and
and 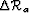 is given by the
is given by the  phase-shift between the
two image perturbations.
phase-shift between the
two image perturbations.





Next: Sensitivity kernels examples
Up: WEMVA sensitivity kernels
Previous: WEMVA sensitivity kernels
Stanford Exploration Project
11/4/2004


![]() is represented by traveltime differences
between recorded and computed traveltimes in a reference medium.
The sensitivity kernels are infinitely-thin rays
computed by ray tracing in the background medium.
For finite-frequency traveltime tomography
(28; 52; 58; 76),
is represented by traveltime differences
between recorded and computed traveltimes in a reference medium.
The sensitivity kernels are infinitely-thin rays
computed by ray tracing in the background medium.
For finite-frequency traveltime tomography
(28; 52; 58; 76),
![]() is represented by time shifts
measured by crosscorelation between the recorded wavefield
and a wavefield computed in a reference medium.
The sensitivity kernels are represented by hollow fat rays
(a.k.a. ``banana-doughnuts'') which depend on the background medium.
For wave-equation tomography
(114; 72; 73),
is represented by time shifts
measured by crosscorelation between the recorded wavefield
and a wavefield computed in a reference medium.
The sensitivity kernels are represented by hollow fat rays
(a.k.a. ``banana-doughnuts'') which depend on the background medium.
For wave-equation tomography
(114; 72; 73),
![]() is represented by perturbations
between the recorded wavefield and the computed wavefield
in a reference medium.
The sensitivity kernels are represented by fat rays with similar forms
for either the Born or Rytov approximation.
For wave-equation migration velocity analysis
(10; 88; 89; 93),
is represented by perturbations
between the recorded wavefield and the computed wavefield
in a reference medium.
The sensitivity kernels are represented by fat rays with similar forms
for either the Born or Rytov approximation.
For wave-equation migration velocity analysis
(10; 88; 89; 93),
![]() is represented by image perturbations.
The sensitivity kernels are discussed in the following sections.
is represented by image perturbations.
The sensitivity kernels are discussed in the following sections.
![]() and
perturbations of migrated images
and
perturbations of migrated images ![]() .
.![]() and
and ![]() correspond, respectively, to
correspond, respectively, to ![]() and
and ![]() in linear.
in linear.
![]() depends on
the wavefield computed by extrapolation of the surface
data using the background slowness,
which corresponds to
depends on
the wavefield computed by extrapolation of the surface
data using the background slowness,
which corresponds to ![]() in frechet.exp.
Thus, the operator
in frechet.exp.
Thus, the operator ![]() depends directly on the type of
recorded data and its frequency content,
and it also depends on the background slowness model.
Thus, the main elements that control the shape
of the sensitivity kernels are
depends directly on the type of
recorded data and its frequency content,
and it also depends on the background slowness model.
Thus, the main elements that control the shape
of the sensitivity kernels are
![]() , implemented simply as a derivative
of the image with respect to depth, which can be implemented as
a multiplication in the depth domain as follows:
, implemented simply as a derivative
of the image with respect to depth, which can be implemented as
a multiplication in the depth domain as follows: