




Next: WEMVA objective function
Up: Wave-equation migration velocity analysis
Previous: Introduction
Imaging by wavefield extrapolation (WE) is based on recursive
continuation of the wavefields (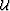 ) from a given depth level
to the next by means of an extrapolation operator (
) from a given depth level
to the next by means of an extrapolation operator (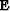 ):
):
| 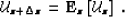 |
(45) |
Here and hereafter, I use the following notation conventions:
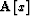 means operator
means operator 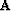 applied to x, and
applied to x, and
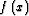 means function f of argument x.
The subscripts
means function f of argument x.
The subscripts  or
or 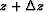 indicate quantities corresponding
to the depth levels
indicate quantities corresponding
to the depth levels  and
and 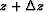 , respectively.
, respectively.
This recursive down can also be explicitly written in
matrix form as
-_0-_1-_n-1 _0_1_2_n = _0 0 0 0 ,
or in a more compact notation as:
| 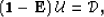 |
(46) |
where the vector 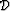 stands for data,
stands for data,
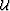 for the extrapolated wavefield at all depth levels,
for the extrapolated wavefield at all depth levels,
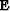 for the extrapolation operator and
for the extrapolation operator and
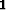 for the identity operator.
Here and hereafter, I make the distinction between
quantities measured at a particular depth level (e.g.
for the identity operator.
Here and hereafter, I make the distinction between
quantities measured at a particular depth level (e.g. 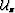 ),
and the corresponding vectors denoting such quantities at all
depth levels (e.g.
),
and the corresponding vectors denoting such quantities at all
depth levels (e.g. 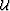 ).
).
After wavefield extrapolation, we can obtain an image
by applying, at every depth level, an imaging operator (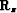 ) to
the extrapolated wavefield
) to
the extrapolated wavefield 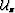 :
:
| 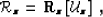 |
(47) |
where 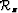 stands for the image at some depth level.
A commonly used imaging operator (
stands for the image at some depth level.
A commonly used imaging operator (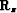 ) involves summation
over the temporal frequencies.
We can write the same relation in compact matrix form as:
) involves summation
over the temporal frequencies.
We can write the same relation in compact matrix form as:
| 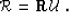 |
(48) |
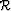 stands for the image, and
stands for the image, and
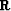 stands for the imaging operator which is
applied to the extrapolated wavefield
stands for the imaging operator which is
applied to the extrapolated wavefield 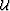 at all
depth levels.
at all
depth levels.
A perturbation 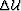 of the wavefield at some depth level can
be derived from the background wavefield
by a simple application of the chain rule to down:
of the wavefield at some depth level can
be derived from the background wavefield
by a simple application of the chain rule to down:
| 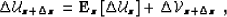 |
(49) |
where 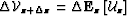 represents the scattered wavefield
generated at
represents the scattered wavefield
generated at 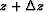 by the interaction of the wavefield
by the interaction of the wavefield 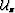 with a perturbation of the velocity model at depth
with a perturbation of the velocity model at depth  .
.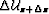 is the accumulated wavefield perturbation
corresponding to slowness perturbations at all levels above.
It is computed by extrapolating the wavefield perturbation
is the accumulated wavefield perturbation
corresponding to slowness perturbations at all levels above.
It is computed by extrapolating the wavefield perturbation 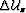 from the level above, plus the scattered wavefield
from the level above, plus the scattered wavefield 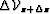 at this level.
at this level.
wavpert is also a recursive equation which can be
written in matrix form as
-_0-_1-_n-1 _0_1_2_n = _0 _1_n-1 _0_1_2_n ,
or in a more compact notation as:
| 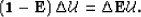 |
(50) |
The operator 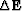 stands for a
perturbation of the extrapolation operator
stands for a
perturbation of the extrapolation operator 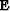 .The quantity
.The quantity 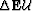 represents a scattered
wavefield, and is a function
of the perturbation in the medium by the
scattering relations derived in Appendix C.
For the case of single scattering, we can write that
represents a scattered
wavefield, and is a function
of the perturbation in the medium by the
scattering relations derived in Appendix C.
For the case of single scattering, we can write that
| 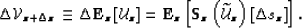 |
(51) |
The expression for the total wavefield perturbation 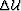 from
wavpert becomes
from
wavpert becomes
| 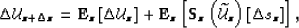 |
(52) |
which is also a recursive relation that can be written in matrix
form as
-_0-_1-_n-1 _0_1_2_n = _0 _1 _n-1 _0 _1 _2 _n s_0s_1s_2s_n ,
or in a more compact notation as:
| 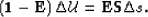 |
(53) |
The vector 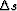 stands for the slowness perturbation at all depths.
stands for the slowness perturbation at all depths.
Finally, if we introduce the notation
| 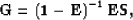 |
(54) |
we can write a simple relation between a slowness perturbation 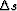 and the corresponding wavefield perturbation
and the corresponding wavefield perturbation 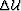 :
:
| 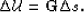 |
(55) |
This expression describes wavefield scattering caused by the interaction
of the background wavefield with a perturbation of the medium.





Next: WEMVA objective function
Up: Wave-equation migration velocity analysis
Previous: Introduction
Stanford Exploration Project
11/4/2004
![]() ) to
the extrapolated wavefield
) to
the extrapolated wavefield ![]() :
:
![]() of the wavefield at some depth level can
be derived from the background wavefield
by a simple application of the chain rule to down:
of the wavefield at some depth level can
be derived from the background wavefield
by a simple application of the chain rule to down:
![]() from
wavpert becomes
from
wavpert becomes