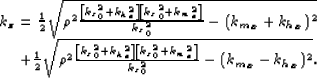Next: Common-azimuth Stolt residual migration
Up: Prestack residual migration
Previous: Stolt migration
In general, residual migration improves the quality of an image
without re-migration of the original data; instead, a transformation
is applied to the current migrated image.
In prestack Stolt residual migration, we attempt to correct
the effects of migrating with an inaccurate reference velocity by
applying a transformation to images transformed to the
Fourier domain.
Supposing that the initial
migration was done with the velocity v0, and that the correct
velocity is v, we can use dsr-sg
to derive 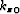 , the vertical wavenumber for the reference
velocity, and
, the vertical wavenumber for the reference
velocity, and 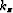 , the vertical wavenumber for the correct velocity.
, the vertical wavenumber for the correct velocity.
Mathematically, the goal of prestack Stolt residual migration
is to obtain 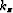 from
from 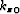 .
If we elliminate
.
If we elliminate  from
from 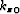 and
and 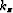 ,and make the notation
,and make the notation 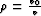 ,we obtain the residual migration equation for full 3D
prestack seismic images:
,we obtain the residual migration equation for full 3D
prestack seismic images:
| 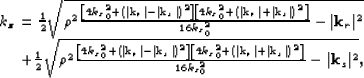 |
(33) |
which can also be represented in midpoint-offset coordinates using the
change of variables in changevar.
If we make the change of variables
| 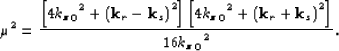 |
(34) |
we obtain a simplified version of myresmig-3d-pr:
| 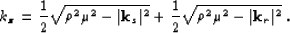 |
(35) |
In the 3D post-stack case, when 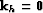 ,
myresmig-3d-pr becomes:
,
myresmig-3d-pr becomes:
| 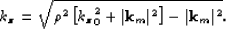 |
(36) |
In the 2D prestack case (kmy=0 and kmx=0),
we can write myresmig-3d-pr as:
| 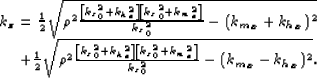 |
(37) |
For 2D post-stack data, myresmig-3d-po and myresmig-2d-pr become
| 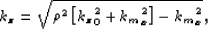 |
(38) |
which can also be written in the familiar form (102):
| 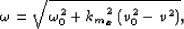 |
(39) |
where, by definition, 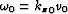 , and
, and 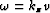 .
.





Next: Common-azimuth Stolt residual migration
Up: Prestack residual migration
Previous: Stolt migration
Stanford Exploration Project
11/4/2004
![]() , the vertical wavenumber for the reference
velocity, and
, the vertical wavenumber for the reference
velocity, and ![]() , the vertical wavenumber for the correct velocity.
, the vertical wavenumber for the correct velocity.
![]() from
from ![]() .
If we elliminate
.
If we elliminate ![]() from
from ![]() and
and ![]() ,and make the notation
,and make the notation ![]() ,we obtain the residual migration equation for full 3D
prestack seismic images:
,we obtain the residual migration equation for full 3D
prestack seismic images:
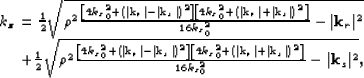
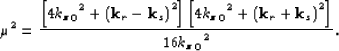
![]() ,
myresmig-3d-pr becomes:
,
myresmig-3d-pr becomes: