




Next: Computing the traveltime: an
Up: Liner and Vlad: Multiple
Previous: Cascading image-construction operations
Let us denote by n a value smaller 1 less than
the total number of bounces of the wave in the earth. Let us pretend
``not to know'' that the horizontal coordinates of S and G are
-h and h, respectively, and denote them with s and g instead,
since we will later need a more general expression that can be
differentiated with respect to these variables. We start by generating
the sequences 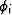 and li, according to (5) and
(6), and keeping in mind the nonphysical prependix
and li, according to (5) and
(6), and keeping in mind the nonphysical prependix 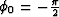 .
.
Using the fact that n is always even because the total number of
bounces inside the earth is always odd, and substituting into
(25), we find the image cascaded through n reflection
operations from the source to be
| ![\begin{displaymath}
{\bf q}_n^S = s \left[ {\begin{array}
{*{20}c}
{-\sin\beta_n...
..._j} \\ {\left(-1\right)^j \cos\beta_j} \\ \end{array}} \right].\end{displaymath}](img36.gif) |
(27) |
The receiver image is obtained from a single reflection
operation, through the last reflecting interface:
| ![\begin{displaymath}
{\bf q}_1^G=g\left[ {\begin{array}
{*{20}c}{\cos2\phi_{n+1}}...
...{-\sin\phi_{n+1}} \\ {\cos\phi_{n+1}}
\\ \end{array}} \right].\end{displaymath}](img37.gif) |
(28) |
The traveltime is the distance between 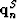 and
and 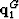 divided by the velocity. This distance will be computed as the magnitude
of the vector
divided by the velocity. This distance will be computed as the magnitude
of the vector 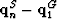 . By making the notations
. By making the notations
| ![\begin{displaymath}
{\bf u}_1 = \frac{2}{v}\left\{\sum\limits_{j=0}^{n-1} l_{n-j...
...i_{n+1}} \\ {-\cos\phi_{n+1}}
\\ \end{array}} \right]\right\},\end{displaymath}](img41.gif) |
(29) |
| ![\begin{displaymath}
{\bf u}_2=\frac{1}{v}\left[ {\begin{array}
{*{20}c}
{-\sin\beta_n} \\ { \cos\beta_n} \\ \end{array}} \right],\end{displaymath}](img42.gif) |
(30) |
| ![\begin{displaymath}
{\bf u}_3=-\frac{1}{v}\left[ {\begin{array}
{*{20}c}{\cos2\phi_{n+1}} \\ {\sin2\phi_{n+1}}
\\ \end{array}} \right],\end{displaymath}](img43.gif) |
(31) |
we can write:
| 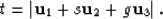 |
(32) |
In particular, for s=-h and g=h and
| ![\begin{displaymath}
{\bf u}_4={\bf u}_2-{\bf u}_3=\frac{1}{v}\left[
{\begin{arr...
...left(-\beta_n\right)+\sin2\phi_{n+1}}
\\ \end{array}} \right],\end{displaymath}](img45.gif) |
(33) |
the traveltime can be written as
| 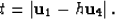 |
(34) |
This vector magnitude can be computed using scalar products:
| ![\begin{displaymath}
t=\sqrt{\left[{\bf u}_1-h{\bf u}_4\right]\cdot\left[{\bf u}_1-h{\bf u}_4\right]}\end{displaymath}](img47.gif) |
(35) |
or it can be written as
| 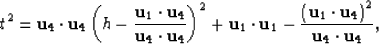 |
(36) |
which is the equation of a hyperbola with the apex at
| 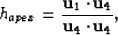 |
(37) |
| 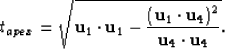 |
(38) |





Next: Computing the traveltime: an
Up: Liner and Vlad: Multiple
Previous: Cascading image-construction operations
Stanford Exploration Project
10/23/2004
![\begin{displaymath}
{\bf q}_n^S = s \left[ {\begin{array}
{*{20}c}
{-\sin\beta_n...
..._j} \\ {\left(-1\right)^j \cos\beta_j} \\ \end{array}} \right].\end{displaymath}](img36.gif)
![\begin{displaymath}
{\bf q}_n^S = s \left[ {\begin{array}
{*{20}c}
{-\sin\beta_n...
..._j} \\ {\left(-1\right)^j \cos\beta_j} \\ \end{array}} \right].\end{displaymath}](img36.gif)
![\begin{displaymath}
{\bf u}_1 = \frac{2}{v}\left\{\sum\limits_{j=0}^{n-1} l_{n-j...
...i_{n+1}} \\ {-\cos\phi_{n+1}}
\\ \end{array}} \right]\right\},\end{displaymath}](img41.gif)