




Next: SECOND DERIVATION
Up: Berryman: Bounds on transport
Previous: THE ANALTYICAL FORMULATION
To obtain some useful bounds, I again consider the form of
(1)
| 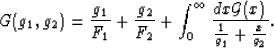 |
(4) |
For reasons that will become apparent I want to compare the values of
G(g1+2g0,g2+2g0) and G(g1,g2)+2g0, where g0 can take any
positive value, but g0 is limited in the negative range by the
limitations that both g1+2g0 and g2+2g0 must always be
nonnegative.
A straightforward, but somewhat tedious calculation shows that
| ![\begin{displaymath}
\begin{array}
{l}
G(g_1+2g_0,g_2+2g_0) - G(g_1,g_2) - 2g_0 =...
...cal
G}(x)}{(1+x)(g_2+xg_1)[g_2+xg_1+2(1+x)g_0]}\, .\end{array} \end{displaymath}](img7.gif) |
(5) |
The right hand side of this equation is always positive whenever g0
>0 and 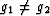 . It vanishes when g0 = 0 or g1 = g2.
If g1 < g2, then for negative values of the parameter g0, allowed
values of g0 lie in the range
. It vanishes when g0 = 0 or g1 = g2.
If g1 < g2, then for negative values of the parameter g0, allowed
values of g0 lie in the range 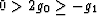 . For such values
of g0, the right hand side of (5) is strictly negative.
. For such values
of g0, the right hand side of (5) is strictly negative.
The limiting case obtained by taking 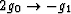 is most useful
because, in this limit,
is most useful
because, in this limit, 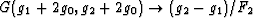 -- thus eliminating the unknown functional
-- thus eliminating the unknown functional 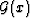 from this
part of the expression. Then, (5) shows that
from this
part of the expression. Then, (5) shows that
| 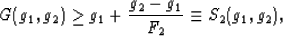 |
(6) |
which is a general lower bound on G(g1,g2) without any further
restrictions on the measurable quantities 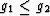 , and F2.
, and F2.
A second bound can be obtained (again in the limit 2g0 = -g1)
by noting that
| 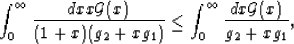 |
(7) |
and then recalling that
| ![\begin{displaymath}
\int_0^\infty \frac{dx {\cal G}(x)}{g_2+xg_1} =
\frac{1}{g_1g_2}\left[G(g_1,g_2) - \frac{g_1}{F_1} -
\frac{g_2}{F_2}\right].
\end{displaymath}](img16.gif) |
(8) |
Substituting (7) into (5) produces an upper
bound on G(g1,g2). By subsequently substituting
(8) and then rearranging the result, the final bound is
| 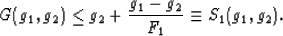 |
(9) |
Comparing (6) and (9), I see consistency
requires that
| 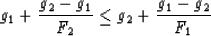 |
(10) |
must be true. Rearranging this expression gives the condition
| 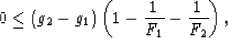 |
(11) |
the validity of which I need to check.
In the limit g1 = g2 = 1, a sum rule follows from
(4), and from this I have:
| 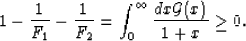 |
(12) |
This shows explicitly that (11) is always
satisfied as long as 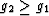 . If this inequality
. If this inequality 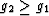 does not hold, then
the sense of the bounding inequalities is changed, so the expressions
for the upper and lower bounds trade places.
does not hold, then
the sense of the bounding inequalities is changed, so the expressions
for the upper and lower bounds trade places.
When 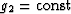 and g1 varies (as would be expected in a series
of thermal conductivity experiments with different fluids in the same
porous medium), then (6) and (9)
are both straight lines that cross at g1 = g2. The general bounds
are therefore
and g1 varies (as would be expected in a series
of thermal conductivity experiments with different fluids in the same
porous medium), then (6) and (9)
are both straight lines that cross at g1 = g2. The general bounds
are therefore
| 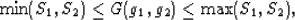 |
(13) |
where S1 and S2 were defined in (6) and
(9).





Next: SECOND DERIVATION
Up: Berryman: Bounds on transport
Previous: THE ANALTYICAL FORMULATION
Stanford Exploration Project
10/23/2004
![\begin{displaymath}
\begin{array}
{l}
G(g_1+2g_0,g_2+2g_0) - G(g_1,g_2) - 2g_0 =...
...cal
G}(x)}{(1+x)(g_2+xg_1)[g_2+xg_1+2(1+x)g_0]}\, .\end{array} \end{displaymath}](img7.gif)
![]() is most useful
because, in this limit,
is most useful
because, in this limit, ![]() -- thus eliminating the unknown functional
-- thus eliminating the unknown functional ![]() from this
part of the expression. Then, (5) shows that
from this
part of the expression. Then, (5) shows that
![]() and g1 varies (as would be expected in a series
of thermal conductivity experiments with different fluids in the same
porous medium), then (6) and (9)
are both straight lines that cross at g1 = g2. The general bounds
are therefore
and g1 varies (as would be expected in a series
of thermal conductivity experiments with different fluids in the same
porous medium), then (6) and (9)
are both straight lines that cross at g1 = g2. The general bounds
are therefore