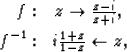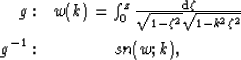Next: Riemannian Wavefield Extrapolation
Up: Shragge and Sava: Migration
Previous: Introduction
Conformal mapping is a topic of wide-spread interest in the field of
applied complex analysis. Generally, this subject deals with the
manner in which point sets are mapped between two different analytic
domains in the complex plane. In this paper, we refer only to domains
that are simply- (i.e. not multiply) connected. A mapping between
complex planes may be thought of as a rule relating how a field of
points defined on a domain in the z-plane, z=x+iy, maps to the
w-plane, w=u(x,y)+iv(x,y), according to a mapping function, w=f(z)
(see the example in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). If for each point in the
z-plane domain there corresponds a unique number in the w-plane,
then the mapping function is analytic. In addition, if for each point
in the w-plane there corresponds precisely one point in the
z-plane, then the mapping is one-to-one and the transformation is
invertible. The Cauchy-Riemann equations Nehari (1975) are the
necessary and sufficient conditions for function f(z) to be analytic
in a domain of interest.
map1
). If for each point in the
z-plane domain there corresponds a unique number in the w-plane,
then the mapping function is analytic. In addition, if for each point
in the w-plane there corresponds precisely one point in the
z-plane, then the mapping is one-to-one and the transformation is
invertible. The Cauchy-Riemann equations Nehari (1975) are the
necessary and sufficient conditions for function f(z) to be analytic
in a domain of interest.
map1
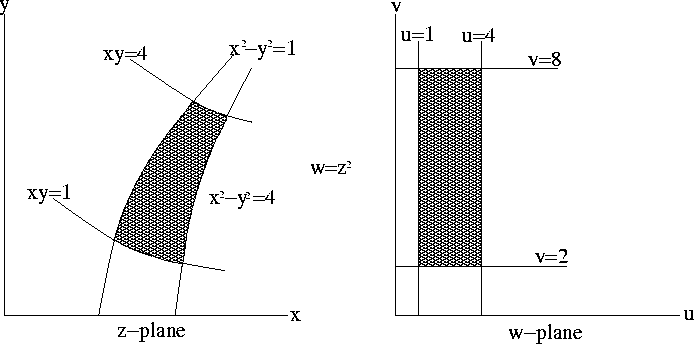
Figure 1 An example of a conformal mapping
between the z-plane, z=x+iy, and the w-plane,
w(z)=u(x,y)+iv(x,y), according to mapping function w=z2. In
this example, the shaded region in the z-plane maps to the shaded
region in the w-plane. Coordinates (u,v) are given by
(x2-y2,2xy). Lines in the w-plane: u=1, u=4, v=2,
and v=8, map to the following lines in the z-plane: x2-y2=1,
x2-y2=4, xy=1. Note also that orthogonality of line
intersections in the w-plane are preserved in the z-plane.

A conformal map is distinguishable from other mappings between complex
planes by characteristic properties. Most important to this
discussion is the following property:
- Conservation of Angle:
- A conformal mapping of two continuous
arcs that locally form an angle
 in the z-plane will
generate two continuous arcs seperated by the same local angle
in the z-plane will
generate two continuous arcs seperated by the same local angle
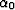 in the w-plane.
in the w-plane.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the property that grid lines
orthogonal in the w-plane are orthogonal in the z-plane under a
conformal map. By extension, non-Cartesian orthogonal coordinate
systems can be created in the z-plane (or conversely in the
w-plane) by a conformal mapping of a rectangular coordinate system
in the w-plane (z-plane).
illustrates the property that grid lines
orthogonal in the w-plane are orthogonal in the z-plane under a
conformal map. By extension, non-Cartesian orthogonal coordinate
systems can be created in the z-plane (or conversely in the
w-plane) by a conformal mapping of a rectangular coordinate system
in the w-plane (z-plane).
The first major developments in the theory of conformal mapping
originated with the mapping theorem of Riemann (1851),
who proved the existence of a unique analytic mapping between any two
simply-connected, analytic domains:
- Riemann Mapping Theorem:
- Let D be a simply-connected
region. Then there exists a bijective conformal map
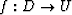 ,where U is the open unit disk. By extension, if G is
a another simply-connected domain, there exists a mapping
,where U is the open unit disk. By extension, if G is
a another simply-connected domain, there exists a mapping 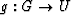 . Hence, there exists a composite mapping operation,
. Hence, there exists a composite mapping operation,
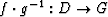 , between two arbitrary
simply-connected domains.
, between two arbitrary
simply-connected domains.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the Riemann mapping
theorem between three domains pertinent to the current discussion.
Figure
illustrates the Riemann mapping
theorem between three domains pertinent to the current discussion.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) presents an example of a conformal mapping
between a square and unit circule (the mapping g in
Figure
presents an example of a conformal mapping
between a square and unit circule (the mapping g in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
Riemap
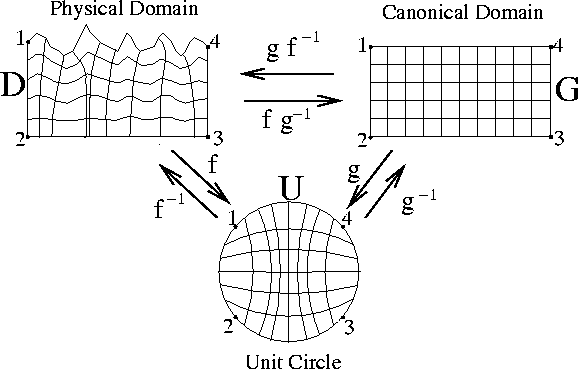
Figure 2 Illustration of the Riemann Mapping Theorem
between a physical domain with an undulating upper surface, the unit
circle, and a rectangular canonical domain. In this example, a
forward mapping function, f, exists between the physical domain
and the unit circle and, because the mapping is one-to-one, an
inverse mapping f-1 also exists. Forward and inverse mapping
functions (g and g-1) also exist between the rectilinear
domain and the unit circle. Hence, the composition of functions 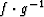 denotes a mapping between the physical and canonical
domains, while the inverse mapping is given by
denotes a mapping between the physical and canonical
domains, while the inverse mapping is given by 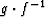 . The mapping locations of points labeled 1 through 4 are specified to
ensure that the sides in the physical domain correspond to the
sides in the canonical domain.
. The mapping locations of points labeled 1 through 4 are specified to
ensure that the sides in the physical domain correspond to the
sides in the canonical domain.

We will use the Riemann mapping theorem to transform the topographic
domain to a rectangular computational mesh. Assisting us is an extensive
catalog of conformal maps between common geometrical domains.
Pertinent to the current discussion are the conformal maps between the
unit circle (UC) and the upper half plane (UHP), 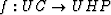 and its inverse
and its inverse 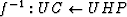 ,
,
| 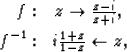 |
(1) |
| |
and the mapping between the UHP and a rectangle with sides of
arbitrary length, 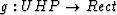 , and its inverse
, and its inverse 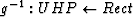 ,
,
| 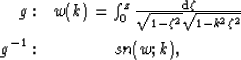 |
(2) |
| |
where g is an elliptic integral of the first kind, k is a function
of the ratio of the length of the two sides, and sn(w;k) is a
Jacobian elliptic function Nehari (1975). Appendix A discusses
a method for computing conformal map transforms between arbitrary
polygons and the UHP.
confexamp
Figure 3 Conformal mapping between a
square coordinate system and the unit circle.
|
| 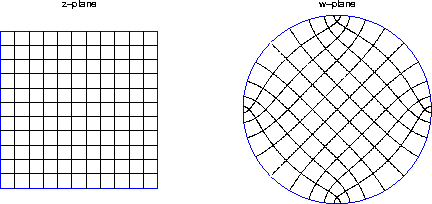 |

Table 1 outlines a work flow to generate a topographic coordinate
system through conformal mapping. The first step is to define
the enclosure of the physical domain where the topographic surface
defines the upper boundary. We create the lower boundary by mirroring
the topography at twice the maximum extrapolation depth. The side
boundaries are defined by straight lines that join the top and bottom
segments. We denote the border points ztopobnd, where
subscript topo and superscript bnd refer to topography and
boundary points, respectively. The four corner points of the physical
domain are also specified. The next two steps involve calculating the
forward and inverse mapping functions, f and f-1, between the
topographic surface and the unit circle. The fourth step is to
generate a rectilinear boundary and to define its four corner points.
We denote this boundary zrectbnd, where subscript rect
refers to rectangle. The next two steps involve calculating forward
and inverse mappings functions, g and g-1, between the boundary
of the rectangle and the unit circle.
To discern where in the canonical domain to form the coordinate system
grid, we need to find the mapping of the topography boundary points on
the rectangular domain boundary. This is accomplished by calculating the
image of the boundary points under composite mapping operations,
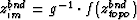 . A rectangular grid is
then set up at the image points to create computational grid,
zrectcs, where superscripts cs denote coordinate
system.
. A rectangular grid is
then set up at the image points to create computational grid,
zrectcs, where superscripts cs denote coordinate
system.
Table 1. Work flow to calculate topographic coordinates with
conformal mapping.
| Step |
Description |
Notation |
| 1 |
Define physical domain boundary and 4 corner points |
ztopobnd |
| 2 |
Calculate mapping 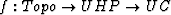 |
wtopobnd=f(ztopobnd) |
| 3 |
Calculate mapping 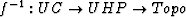 |
ztopobnd=f-1(wtopobnd) |
| 4 |
Define canonical domain border and 4 corner points |
zrectbnd |
| 5 |
Calculate mapping 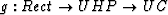 |
wrectbnd=g(zrectbnd) |
| 6 |
Calculate mapping 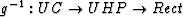 |
zrectbnd=g-1(wrectbnd) |
| 7 |
Find image of topography in the rectangle |
zimbnd=g-1(f(ztopobnd)) |
| 8 |
Construct rectilinear grid using zimbnd(ztopobnd) |
zrectcs |
| 9 |
Map grid zrectcs to physical domain |
ztopocs=f-1(g(zrectcs)) |
The final step is to map the rectilinear coordinate system,
zrectcs, from the canonical domain back to the topographic
coordinates under composite mapping operation, 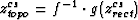 . Point set ztopocs defines a
coordinate system appropriate for performing wavefield continuation
directly from topography at the acquisition locations. The next
section details how this point set is used to generate the appropriate
extrapolation equations.
. Point set ztopocs defines a
coordinate system appropriate for performing wavefield continuation
directly from topography at the acquisition locations. The next
section details how this point set is used to generate the appropriate
extrapolation equations.





Next: Riemannian Wavefield Extrapolation
Up: Shragge and Sava: Migration
Previous: Introduction
Stanford Exploration Project
10/23/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). If for each point in the
z-plane domain there corresponds a unique number in the w-plane,
then the mapping function is analytic. In addition, if for each point
in the w-plane there corresponds precisely one point in the
z-plane, then the mapping is one-to-one and the transformation is
invertible. The Cauchy-Riemann equations Nehari (1975) are the
necessary and sufficient conditions for function f(z) to be analytic
in a domain of interest.
). If for each point in the
z-plane domain there corresponds a unique number in the w-plane,
then the mapping function is analytic. In addition, if for each point
in the w-plane there corresponds precisely one point in the
z-plane, then the mapping is one-to-one and the transformation is
invertible. The Cauchy-Riemann equations Nehari (1975) are the
necessary and sufficient conditions for function f(z) to be analytic
in a domain of interest.