Next: Impulse response tests
Up: Shan and Biondi: Anisotropic
Previous: Extrapolation operator in laterally
Explicit extrapolation operators have been proved useful in isotropic wavefield extrapolation
Hale (1991); Hale (1991); Blacquiere et al. (1989); Holberg (1988); Thorbecke (1997). They
are also applied in wavefield extrapolation for TI media Zhang et al. (2001).
For an isotropic or VTI medium, the extrapolation operator is symmetric and can be approximated by
a cosine function series.
For a tilted TI medium, kz is not an even function
of kx, and the extrapolation operator is asymmetric.
Thus, we need both the sine and cosine function series to approximate the correction operator
in the wavenumber domain.
In equation (6), F(kx) is not an even function, but
can be divided F(kx) into two parts: even function Fe(kx) and odd function Fo(kx),
| 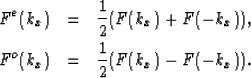 |
(8) |
| (9) |
To design the explicit correction operator, we specify Fe(kx) in the form
| 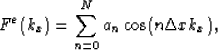 |
(10) |
and Fo(kx) in the form
| 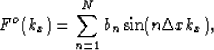 |
(11) |
where an,bn are complex coefficients.
These coefficients can be determined by the following weighted least-squares fitting goals:
| 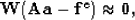 |
(12) |
| 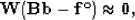 |
(13) |
where
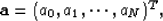
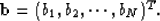
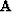 is an
is an 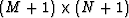 matrix with elements
matrix with elements 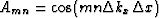 ,
, 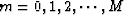 , and
, and
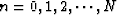 .
.
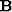 is
an
is
an 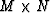 matrix with elements
matrix with elements 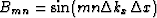 ,
, 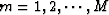 , and
, and 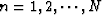 .
. 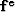 is a vector
with elements
is a vector
with elements 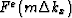 ,
, 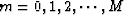 .
. 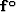 is a vector with elements
is a vector with elements
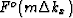 ,
, 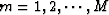 .
. 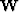 is a diagonal matrix with proper weights for the wavenumber kx.
One way to solve the fitting goal (12) is to do QR decomposition Golub and Van Loan (1996) of the matrix
is a diagonal matrix with proper weights for the wavenumber kx.
One way to solve the fitting goal (12) is to do QR decomposition Golub and Van Loan (1996) of the matrix 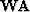 :
: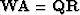 , where
, where 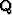 is an orthogonal matrix and
is an orthogonal matrix and 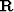 is an upper triangular matrix.
Then the coefficient vector
is an upper triangular matrix.
Then the coefficient vector  is given by
is given by
| 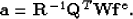 |
(14) |
We can solve the fitting goal in equation (13) and obtain the coefficient vector 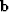 in the same way.
After we have the coefficient
vectors
in the same way.
After we have the coefficient
vectors  and
and 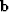 , we can combine them into the coefficients for the explicit correction operator.
From Fourier transform theory, it is well known that the inverse Fourier transform of the function
, we can combine them into the coefficients for the explicit correction operator.
From Fourier transform theory, it is well known that the inverse Fourier transform of the function 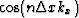 and
and 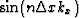 are:
are:
| 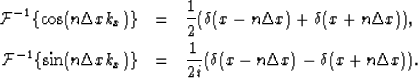 |
(15) |
| (16) |
Thus,
the inverse Fourier transform of the function 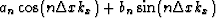 is
is
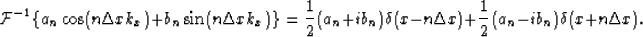
Therefore, the explicit correction operator is:
| 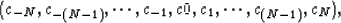 |
(17) |
where c0=a0, and
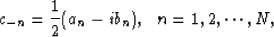
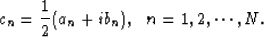
In 3-D, based on the following trigonometric identity,
| ![\begin{displaymath}
\cos (n \theta)=2\cos(\theta)\cos[(n-1)\theta]-\cos[(n-2)\theta],\end{displaymath}](img54.gif) |
(18) |
we can run McClellan transformations Hale (1991); McClellan and Chan (1977); McClellan and Parks (1972) for the cosine terms.
Similarly, based on the trigonometric identity:
| ![\begin{displaymath}
\sin (n \theta)=2\cos(\theta)\sin[(n-1)\theta]-\sin[(n-2)\theta],\end{displaymath}](img55.gif) |
(19) |
we can design a recursive operator similar to McClellan transformations for the sine terms.
ico
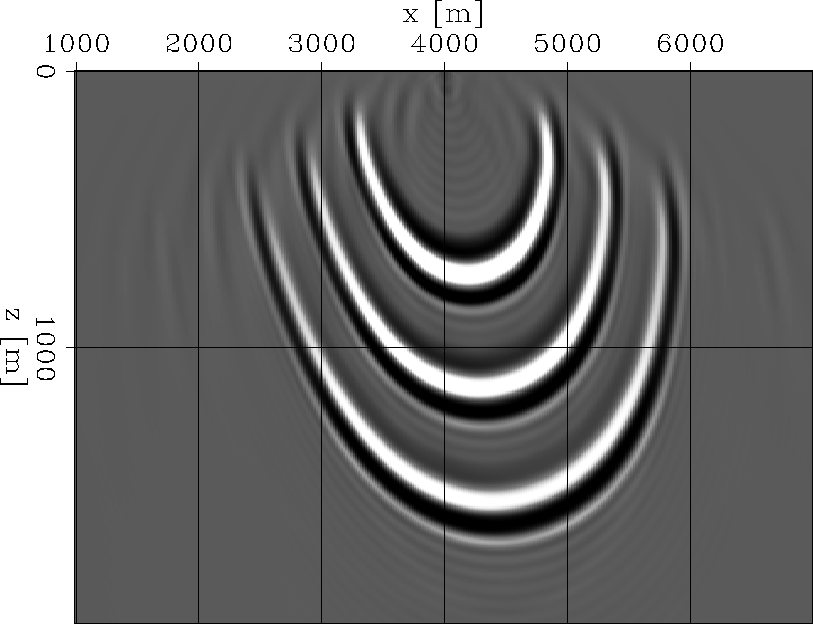
Figure 1 Impulse response of isotropic phase-shift with an anisotropic correction operator.




 icoffd
icoffd
Figure 2 Impulse response of isotropic FFD with an anisotropic correction operator.




 phsift
phsift
Figure 3 Impulse response of anisotropic phase-shift.










Next: Impulse response tests
Up: Shan and Biondi: Anisotropic
Previous: Extrapolation operator in laterally
Stanford Exploration Project
10/23/2004
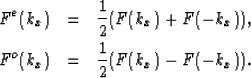
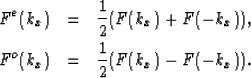
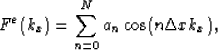
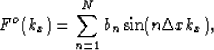
![]()
![]()
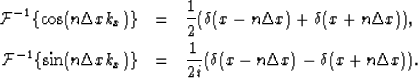
![]()
![]()
![]()