




Next: Explicit correction operator
Up: Shan and Biondi: Anisotropic
Previous: Anisotropic phase-shift in tilted
The phase-shift method is effective, but it is not suitable for a strongly heterogeneous medium, where strong
lateral changes are present in velocity as well as in the anisotropy parameters,  and
and 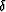 .This can be remedied by PSPI Rousseau (1997), explicit operator Zhang et al. (2001),
or reference anisotropic phase-shift with an explicit correction filter Baumstein and Anderson (2003).
.This can be remedied by PSPI Rousseau (1997), explicit operator Zhang et al. (2001),
or reference anisotropic phase-shift with an explicit correction filter Baumstein and Anderson (2003).
In this paper, we use an explicit anisotropic correction filter in addition
to the normal isotropic operator.
For each z step, we first regard the medium as an isotropic medium and extrapolate
the wavefield using an isotropic operator with the velocity in the direction parallel
to the symmetry axis.
The isotropic operator can be the split-step method Stoffa et al. (1990),
the general screen propagator Huang and Wu (1996),
or Fourier finite difference (FFD) Ristow and Ruhl (1994).
Then we correct the wavefield with an explicit correction operator.
After we extrapolate
the wavefield with an isotropic operator, the resulting error relative to
anisotropic extrapolation is:
| 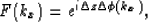 |
(6) |
where 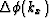 is the difference between the isotropic wavenumber, kzi,
and the anisotropic wavenumber, kza, that satisfies
is the difference between the isotropic wavenumber, kzi,
and the anisotropic wavenumber, kza, that satisfies
| 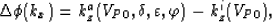 |
(7) |
where,
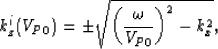
and kza is one of the four roots of the dispersion-relation
equation (4). We design the explicit correction operator by weighted least squares.
The obtained explicit operator is approximately the same as F(kx)
in the wavenumber domain for desired wavenumbers.





Next: Explicit correction operator
Up: Shan and Biondi: Anisotropic
Previous: Anisotropic phase-shift in tilted
Stanford Exploration Project
10/23/2004
![]()