




Next: Tomography
Up: R. Clapp: Velocity uncertainty
Previous: INTRODUCTION
In inversion we try to estimate some model 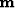 given
some data
given
some data 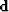 and an operator
and an operator 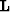 that maps
between the quantities.
If our problem is poorly constrained, we can employ
Tikhonov regularization Tikhonov and Arsenin (1977), adding a roughening
operator
that maps
between the quantities.
If our problem is poorly constrained, we can employ
Tikhonov regularization Tikhonov and Arsenin (1977), adding a roughening
operator 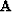 to our objective function Q.
To balance the two components of the objective
function we introduce a twiddle parameter
to our objective function Q.
To balance the two components of the objective
function we introduce a twiddle parameter  and end up with
and end up with
| 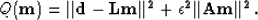 |
(1) |
The two terms in our objective function serve different purposes.
The first deals with data fitting and the second
model styling. We can write the minimization in a slightly
different form in terms of two fitting goals,
| 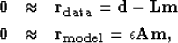 |
(2) |
| |
where  is a vector of zeros,
is a vector of zeros, 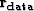 is the data residual
vector, and
is the data residual
vector, and 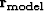 is the model.
Our regularization operator, at best, usually only
accounts for second order statistics, producing a model
that is often unrealistic.
In previous papers Clapp (2000, 2001a) I showed
how by adding Gaussian random noise to the
is the model.
Our regularization operator, at best, usually only
accounts for second order statistics, producing a model
that is often unrealistic.
In previous papers Clapp (2000, 2001a) I showed
how by adding Gaussian random noise to the 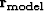 we
can add variance to our models and give the a more
realistic texture.
we
can add variance to our models and give the a more
realistic texture.
If we decorrelate our data residual vector by
adding an inverse noise covariance operator 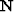 ,
,
| 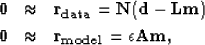 |
(3) |
| |
we can account for uncertainty in our data Clapp (2001b).
This is similar, but not the same as, using stochastic
simulation Isaaks and Srivastava (1989a,b) to create several different datasets.
The two most notable differences are that we
can handle much more spatially variant and
complex covariance descriptions and we have the effect
of a model styling goal in our inversion.
![]() ,
,