Example

This example is taken from Claerbout (1999) and is completely inappropriate for an out-of-core solver. It is a simple 1-D interpolation problem that takes a second to run on a modern computer and takes 5 minutes to run out-of-core. I am using it because of the simplicity of the concepts. We begin by grabbing all of the command line arguments and checking to make sure data and model are specified.

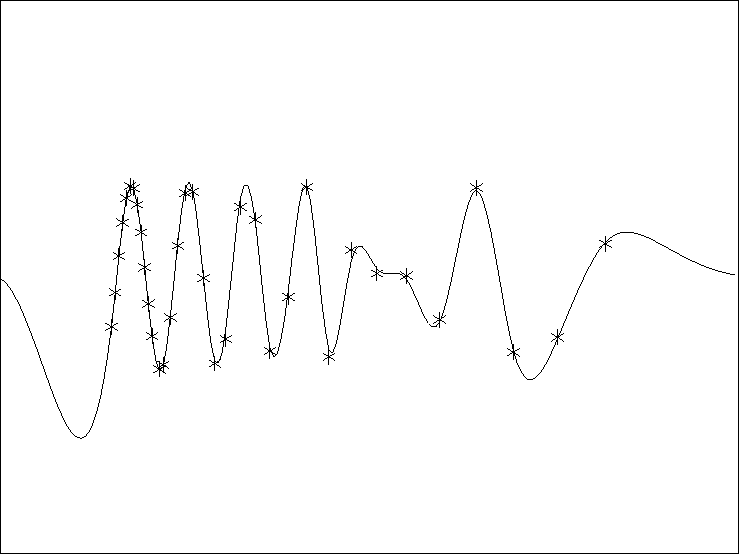args=SEP.par.sep_args() #get arguments
dname=args.par("data",error=1)
mname=args.par("model",error=1)

We then create the data and model float vectors. In the case of the data is read from a file and the model is defined.

data =SEP.sep_vector.sfloat(tag=dname)
model=SEP.sep_vector.sfloat(name=mname)
model.set_axis(200,0.,.4)

We then write out the description of the model to disk and zero the file.

model.write_file()
model.zero()

Our data fitting operator is simple linear interpolation. It takes the coordinates of the data as input and we direct the stdout to /dev/null.

interp_args=SEP.par.sep_pars(name="interp")
interp_args.add_string("coord=coord.H")
interp_args.add_param(">","/dev/null")

We create the argument list for the preconditioner. In this case we just need to direct stdout to /dev/null and specify the type of filter.

precpar=SEP.par.sep_pars(name="devnull")
precpar.add_param("filter",2)0
precpar.add_param(">","/dev/null")0

Next we create our operator objects. In both cases the domain vector is the model. In the case of the interpolation operator the range is the data. For the preconditioning the range is also described by the model space.

interp=SEP.operator.oc("Interp1.x",model,data,pars=interp_args)
prec=SEP.operator.oc("prec.x",model,model,pars=precpar)

We create our step function.

step=SEP.cgstep.cgstep("matcg")

Finally we create our solver object and iterate for 20 iterations. Figure  shows the result of the inversion. The `*' are the known data and the line is the estimated curve.

 

inverse Figure 1 A simple linear interpolation result unsing the out-of-core library.The `*' are the known data and the line is the estimated curve.

solver=SEP.solver.prec("interp1d",model,data,interp,prec,step,20,.1,verb=0)
if not solver.solve():
  SEP.util.err( "Trouble iterating")