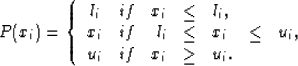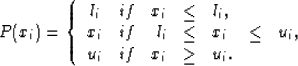Next: Trust region methods
Up: Optimization
Previous: The problem
Identifying A(x) is a minimization problem in itself. An effective
way to find A(x) is by using the gradient projection method Kelley (1999).
First, define P as the projection onto  of
of  such
that for each xi we have
such
that for each xi we have
| 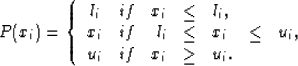 |
(3) |
From this definition, one can modify the classical steepest descent
algorithm by projecting it onto the feasible region as follows:
| 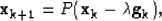 |
(4) |
where k is the iteration number, 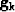 is the gradient of
is the gradient of 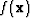 at iteration k and
at iteration k and 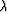 is the step-length given by a
line search scheme. Given the current position
is the step-length given by a
line search scheme. Given the current position
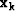 , finding the local minimizer is relatively
straightforward. The important property of the projection algorithm
is that the active set after many iterations is the same as the
active set of the solution vector
, finding the local minimizer is relatively
straightforward. The important property of the projection algorithm
is that the active set after many iterations is the same as the
active set of the solution vector 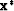 . Then, the exact
solution of the projected gradient is not needed and only an
approximate one is. Then, the inactive
set can be optimized for the unconstrained variables, the
bounded variables being held fixed. The unconstrained
problem can be solved by any method for
unconstrained optimization. The method in this paper
is based on a trust region method that incorporates two important
variations: first, line searches are used; second, the Hessian of
the objective function (or second derivative) is approximated with
BFGS matrices.
. Then, the exact
solution of the projected gradient is not needed and only an
approximate one is. Then, the inactive
set can be optimized for the unconstrained variables, the
bounded variables being held fixed. The unconstrained
problem can be solved by any method for
unconstrained optimization. The method in this paper
is based on a trust region method that incorporates two important
variations: first, line searches are used; second, the Hessian of
the objective function (or second derivative) is approximated with
BFGS matrices.





Next: Trust region methods
Up: Optimization
Previous: The problem
Stanford Exploration Project
10/23/2004