Next: Sigsbee model
Up: numerical examples
Previous: numerical examples
It is possible to explicitly compute the Hessian for small models, or if a target-oriented strategy is followed. We created a synthetic data set assuming a land-type acquisition geometry: the shots were positioned every  from
from 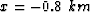 to
to 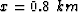 , keeping fixed receivers from
, keeping fixed receivers from 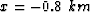 to
to 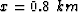 . Figures
. Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a and
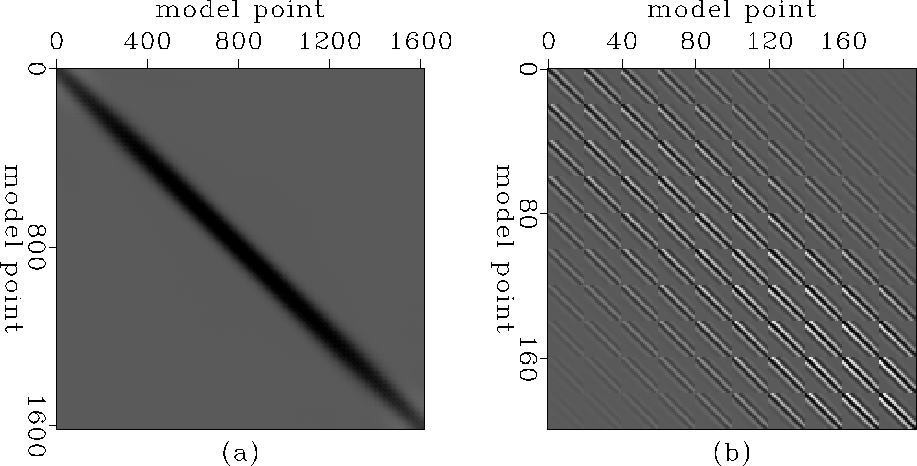
a and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b show the Hessian matrix of the constant-velocity model. Notice the banded nature of the matrix (Figure
b show the Hessian matrix of the constant-velocity model. Notice the banded nature of the matrix (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b), with most of the energy in the main diagonal Chavent and Plessix (1999). At the extremes of the diagonal the amplitudes become dimmer (Figure
b), with most of the energy in the main diagonal Chavent and Plessix (1999). At the extremes of the diagonal the amplitudes become dimmer (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a) indicating points of lower illumination at the extremes of the acquisition.
a) indicating points of lower illumination at the extremes of the acquisition.
hmatrix_const
Figure 1 (a) Hessian matrix of the constant-velocity model, and, (b) close-up of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a.
a.





For a fixed point  , each line of the Hessian
, each line of the Hessian 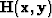 can be mapped to a grid the size of the model space. Figures
can be mapped to a grid the size of the model space. Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
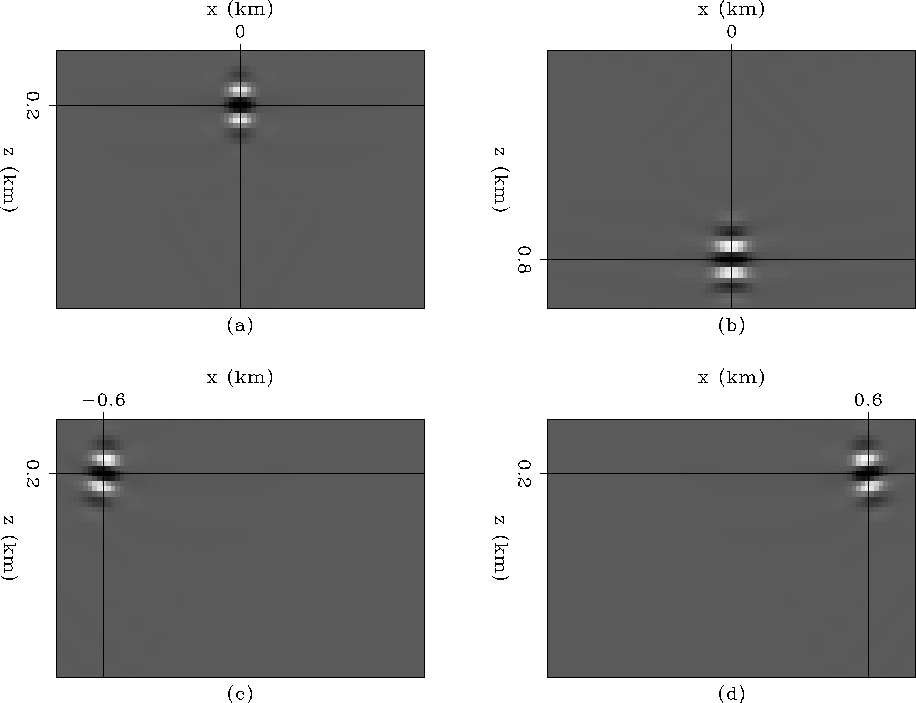
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the Hessian and the envelope of the Hessian at four different fixed points. The Hessian (Figure
show the Hessian and the envelope of the Hessian at four different fixed points. The Hessian (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) has phase information that can make it difficult to interpret in complex subsurface geometries (see Sigsbee and Marmousi model case), therefore we based our analysis looking at the envelope of the Hessian, (Figure
) has phase information that can make it difficult to interpret in complex subsurface geometries (see Sigsbee and Marmousi model case), therefore we based our analysis looking at the envelope of the Hessian, (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which shows clearly the main features of interest.
), which shows clearly the main features of interest.
hesian_phase_const
Figure 2 Hessian of the constant-velocity model, (a) point 1, (b) point 2, (c) point 3, and (d) point 4.





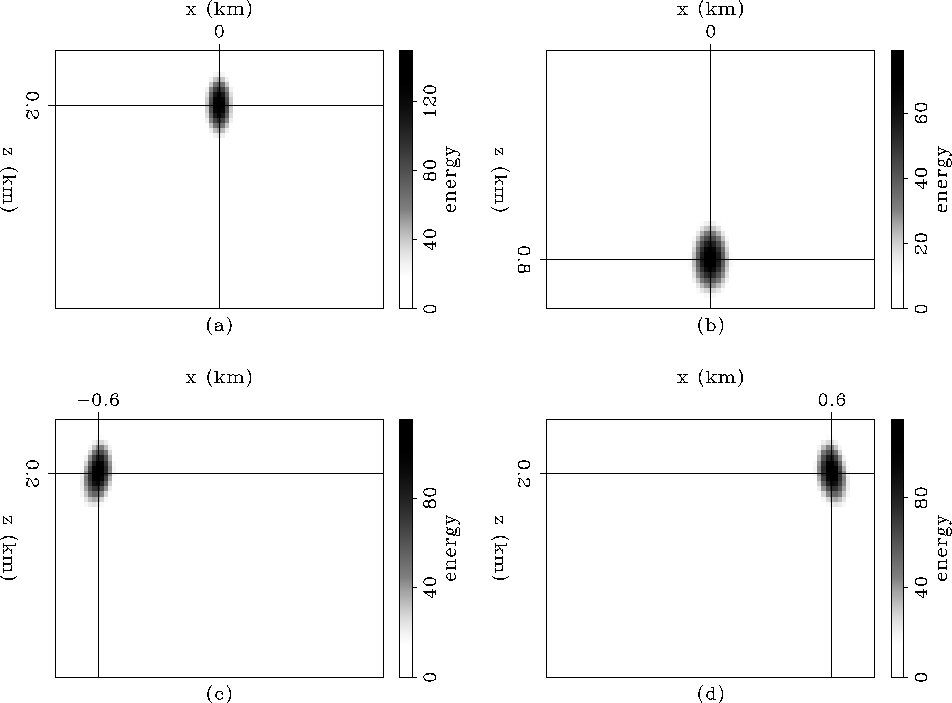
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows point 1, with coordinates
a shows point 1, with coordinates 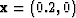 (at the center of the acquisition). Notice the size of the ellipse and the orientation of the principal semi-axis perpendicular to the x axis. Figure
(at the center of the acquisition). Notice the size of the ellipse and the orientation of the principal semi-axis perpendicular to the x axis. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b shows point 2, with coordinates
b shows point 2, with coordinates 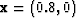 . Notice that the ellipse is bigger than the ellipse corresponding to point 1 (the size of the ellipse depends on the deph and background velocity Chavent and Plessix (1999)), and also that the orientation of the principal semi-axis is perpendicular to the x axis. Figures
. Notice that the ellipse is bigger than the ellipse corresponding to point 1 (the size of the ellipse depends on the deph and background velocity Chavent and Plessix (1999)), and also that the orientation of the principal semi-axis is perpendicular to the x axis. Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c and
c and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d show points 3 and 4, with coordinates
d show points 3 and 4, with coordinates 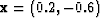 and
and 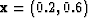 , respectively (opposite sides of the center of the acquisition). Notice the size of the ellipses are the same, but the orientation of the principal semi-axes are tilted in opposite directions. The energy of the ellipses become dimmer than the one in the center, indicating that these points have lower illumination.
, respectively (opposite sides of the center of the acquisition). Notice the size of the ellipses are the same, but the orientation of the principal semi-axes are tilted in opposite directions. The energy of the ellipses become dimmer than the one in the center, indicating that these points have lower illumination.
hesian_const
Figure 3 Envelope of the Hessian of the constant-velocity model, (a) point 1, (b) point 2, (c) point 3, and (d) point 4.










Next: Sigsbee model
Up: numerical examples
Previous: numerical examples
Stanford Exploration Project
10/23/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a and
a and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b show the Hessian matrix of the constant-velocity model. Notice the banded nature of the matrix (Figure
b show the Hessian matrix of the constant-velocity model. Notice the banded nature of the matrix (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b), with most of the energy in the main diagonal Chavent and Plessix (1999). At the extremes of the diagonal the amplitudes become dimmer (Figure
b), with most of the energy in the main diagonal Chavent and Plessix (1999). At the extremes of the diagonal the amplitudes become dimmer (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a) indicating points of lower illumination at the extremes of the acquisition.
a) indicating points of lower illumination at the extremes of the acquisition.