Shuey (1985) showed that in a 1-D earth, the measured reflection strength of an event at the surface is approximately linear with the square of its incidence angle, at angles less than 30 degrees. In a 1-D earth, the NMO equation gives an approximate relationship between offset and incidence angle. Claerbout (1995) defines the ``stepout'', p, as the spatial derivative of an event's traveltime curve:
| |
(37) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In a 1-D earth, the
traveltime curve of a primary reflection is approximately given by the NMO
equation (
. In a 1-D earth, the
traveltime curve of a primary reflection is approximately given by the NMO
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Taking the derivative of equation (
). Taking the derivative of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with
respect to offset, then substituting into equation (
) with
respect to offset, then substituting into equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) gives the
following expression for the sine of incidence angle as a function of offset:
) gives the
following expression for the sine of incidence angle as a function of offset:
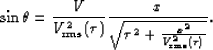 |
(38) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), at which point the AVO ``slope'' and ``intercept''
parameters may be estimated, usually via a linear least-squares fit to the
data after resampling from offset to
), at which point the AVO ``slope'' and ``intercept''
parameters may be estimated, usually via a linear least-squares fit to the
data after resampling from offset to
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the estimation of AVO slope and
intercept parameters on a deep reflector in the Green Canyon 3-D data, before
and after application of LSJIMP. The reflector, which is well under the
multiples in the data, is denoted on the zero offset section with ``O'' symbols.
The maximum amplitude in a small time window around the reflection were picked
automatically, and make up the input data to the least-squares estimation.
illustrates the estimation of AVO slope and
intercept parameters on a deep reflector in the Green Canyon 3-D data, before
and after application of LSJIMP. The reflector, which is well under the
multiples in the data, is denoted on the zero offset section with ``O'' symbols.
The maximum amplitude in a small time window around the reflection were picked
automatically, and make up the input data to the least-squares estimation.
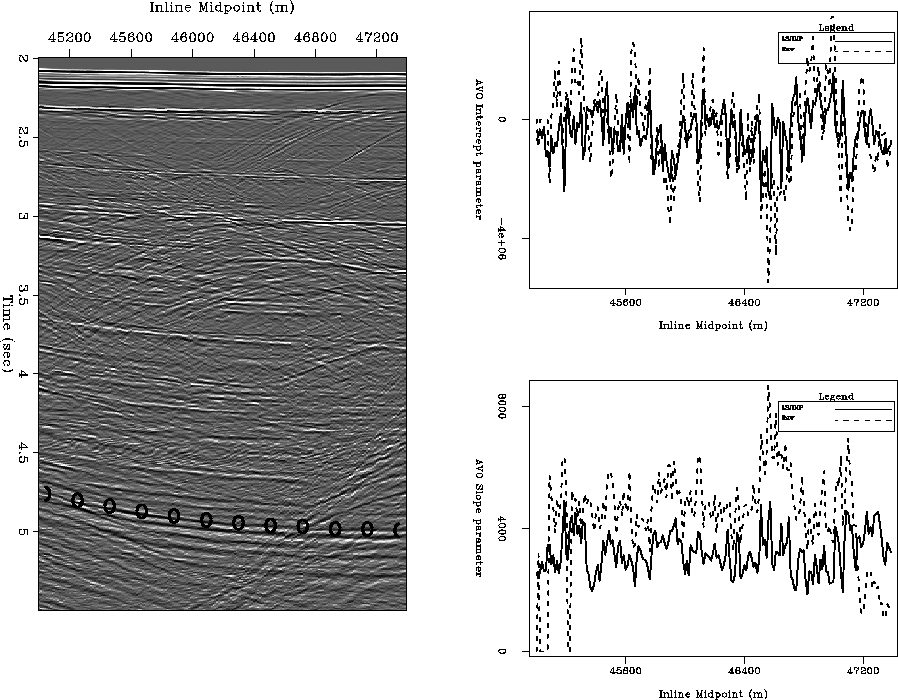 |
We see that while the parameter estimates contain the same trends before and
after LSJIMP, the LSJIMP result is more consistent and less ``noisy'' across
midpoint. My implementation of LSJIMP works on a CMP-by-CMP basis, so the
results shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are not smoothed across
midpoint. The similarity across midpoint is an expression of the true lithology
- lithology which LSJIMP better reveals.
are not smoothed across
midpoint. The similarity across midpoint is an expression of the true lithology
- lithology which LSJIMP better reveals.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates, as a function of midpoint, the
small time windows taken around the deep reflector shown in Figure
illustrates, as a function of midpoint, the
small time windows taken around the deep reflector shown in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , before and after LSJIMP. The input data to an AVO
parameter estimation are picked maximum amplitudes within the time window as a
function of
, before and after LSJIMP. The input data to an AVO
parameter estimation are picked maximum amplitudes within the time window as a
function of ![]() . Notice the significant increase in reflector
clarity after LSJIMP. Also recall that the data residuals (e.g., in Figures
. Notice the significant increase in reflector
clarity after LSJIMP. Also recall that the data residuals (e.g., in Figures
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
are quite small. Therefore, the cleaner reflection events after LSJIMP in
Figure
)
are quite small. Therefore, the cleaner reflection events after LSJIMP in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are not only better for AVO analysis - they
also fit the recorded data in a quantitative fashion. LSJIMP is not an ad
hoc post-processing technique.
are not only better for AVO analysis - they
also fit the recorded data in a quantitative fashion. LSJIMP is not an ad
hoc post-processing technique.
 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , before and after LSJIMP. Individual panels along
the vertical axis correspond to windows taken at different midpoint locations.
Left: Data windows before LSJIMP. Right: Data windows after LSJIMP.
, before and after LSJIMP. Individual panels along
the vertical axis correspond to windows taken at different midpoint locations.
Left: Data windows before LSJIMP. Right: Data windows after LSJIMP.