




Next: AVO Analysis Before and
Up: Results
Previous: Results
Radon demultiple remains the default multiple suppression technique in many
situations, particularly in 3-D, where acquisition sparsity may inhibit other
techniques. On CMP gathers, primaries and multiples normally have different
apparent velocities, and a Radon transform which sums across offset using
various curvature parameters will focus the two types of events in different
parts of the transform panel. The most natural curvature parameter for CMP data
is the velocity of the hyperbola defined by the NMO equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
Foster and Mosher (1992). While the Hyperbolic Radon transform is a linear
mapping, it is not time-invariant, and thus cannot be implemented efficiently as
a Fourier domain operator. However, a multiple's residual moveout after NMO is
approximately parabolic (quadratic) with offset, so a time-invariant Parabolic
Radon transform is much faster, though not as accurate
Hampson (1986); Kabir and Marfurt (1999).
)
Foster and Mosher (1992). While the Hyperbolic Radon transform is a linear
mapping, it is not time-invariant, and thus cannot be implemented efficiently as
a Fourier domain operator. However, a multiple's residual moveout after NMO is
approximately parabolic (quadratic) with offset, so a time-invariant Parabolic
Radon transform is much faster, though not as accurate
Hampson (1986); Kabir and Marfurt (1999).
To remove multiples, the primary energy in the transform panel is muted, and
the inverse radon transform applied to produce an estimate of the multiples,
which is subtracted from the data to produce a primary estimate. If we
define 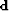 as a raw CMP gather,
as a raw CMP gather, 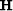 as the linear mapping between radon
transform space and data space,
as the linear mapping between radon
transform space and data space, 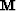 as a mute operator that zeroes primary
energy in radon transform space, and
as a mute operator that zeroes primary
energy in radon transform space, and 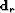 as the estimated primaries,
then we can express the radon demultiple process in equation form:
as the estimated primaries,
then we can express the radon demultiple process in equation form:
| 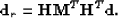 |
(34) |
Operator 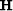 is non-unitary (
is non-unitary ( ), so the
amplitude of the estimated primaries will not match the recorded primaries. By
casting Radon demultiple as a least-squares optimization problem, the Radon
transform panel can be scaled such that
), so the
amplitude of the estimated primaries will not match the recorded primaries. By
casting Radon demultiple as a least-squares optimization problem, the Radon
transform panel can be scaled such that 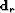 and
and 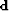 are directly
comparable. We first optimize a Radon transform panel,
are directly
comparable. We first optimize a Radon transform panel, 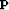 , to minimize the
data misfit:
, to minimize the
data misfit:
| 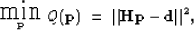 |
(35) |
and then apply the mute operator and adjoint of 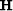 to produce the estimated
primaries:
to produce the estimated
primaries:
| 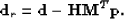 |
(36) |
The finite frequency content of the data, limited extent of the array, and the
intrinsic unresolvability of velocity information at zero offset all contribute
to the non-uniqueness of the least-squares Radon demultiple problem. At far
offsets, events with many zero-offset traveltimes and different velocities are
fit equally well by a single curvature parameter. Low-frequency data makes
moveout discrimination between multiples and primaries more difficult. At near
offsets, all the events are fit equally well by all curvature parameters. All
these pitfalls lead to reduced resolution of events in the Radon domain.
So-called ``high resolution'' least-squares Radon transform implementations
partially overcome these problems by imposing sparsity constraints in either the
hyperbolic or parabolic Radon domain Sacchi and Ulrych (1995); Thorson and Claerbout (1985).
I implemented and tested least-squares Hyperbolic Radon demultiple (LSHRTD) on
the CGG 3-D data subset. I performed 10 conjugate gradient iterations to
produce an optimal 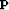 , then applied a mute function which is zero for
velocities greater than 90% known stacking velocity. The mute tapers linearly
from 1.0 to 0.0 between 85% and 90% of the stacking velocity. The
computational cost of LSHRTD is very similar to the cost of applying LSJIMP.
, then applied a mute function which is zero for
velocities greater than 90% known stacking velocity. The mute tapers linearly
from 1.0 to 0.0 between 85% and 90% of the stacking velocity. The
computational cost of LSHRTD is very similar to the cost of applying LSJIMP.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the results of applying LSJIMP and
LSHRTD on a single CMP gather from the CGG 3-D data (CMPx=100, CMPy=4). The
LSHRTD results are quite good, as we expect, given the high velocity gradient
and relatively simple moveout seen in this region of the data. Spatial aliasing
causes some artifacts on the LSHRTD primaries (Figure
compares the results of applying LSJIMP and
LSHRTD on a single CMP gather from the CGG 3-D data (CMPx=100, CMPy=4). The
LSHRTD results are quite good, as we expect, given the high velocity gradient
and relatively simple moveout seen in this region of the data. Spatial aliasing
causes some artifacts on the LSHRTD primaries (Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b)), around
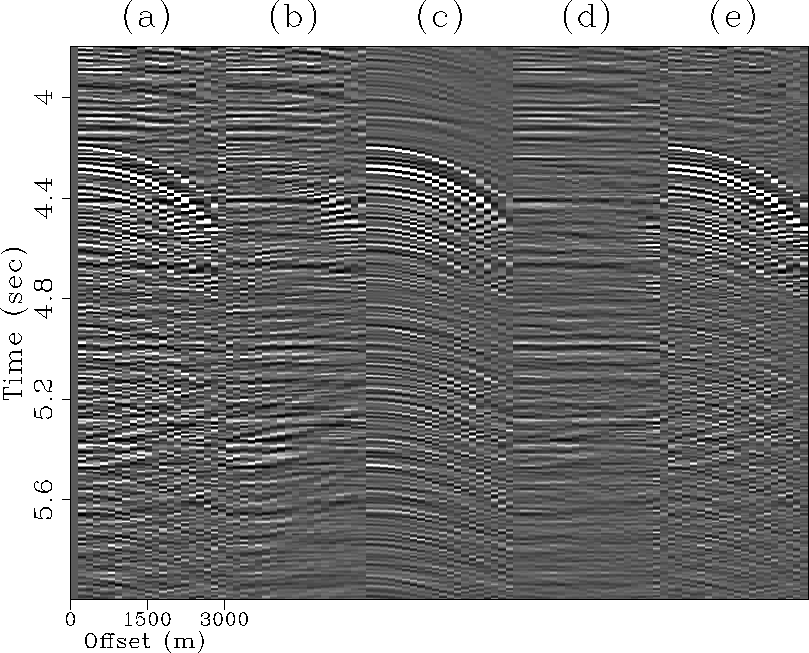
(b)), around 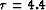 seconds. The radon
primaries seem to contain a bit more spatially uncorrelated noise than the
LSJIMP primaries. LSJIMP is a more ``surgical'' separation technique, although
the model regularization operators also exploit moveout differences to separate
multiples and primaries.
seconds. The radon
primaries seem to contain a bit more spatially uncorrelated noise than the
LSJIMP primaries. LSJIMP is a more ``surgical'' separation technique, although
the model regularization operators also exploit moveout differences to separate
multiples and primaries.
comp.radon.gc3d.100
Figure 8
LSJIMP versus least-squares Hyperbolic Radon demultiple (LSHRTD) on one CMP
gather of the CGG 3-D dataset. Panel (a): Raw data. Panel (b): LSHRTD
estimated primaries. Panel (c): LSHRTD estimated multiples. Panel (d):
LSJIMP estimated primaries. Panel (e): LSJIMP estimated multiples.





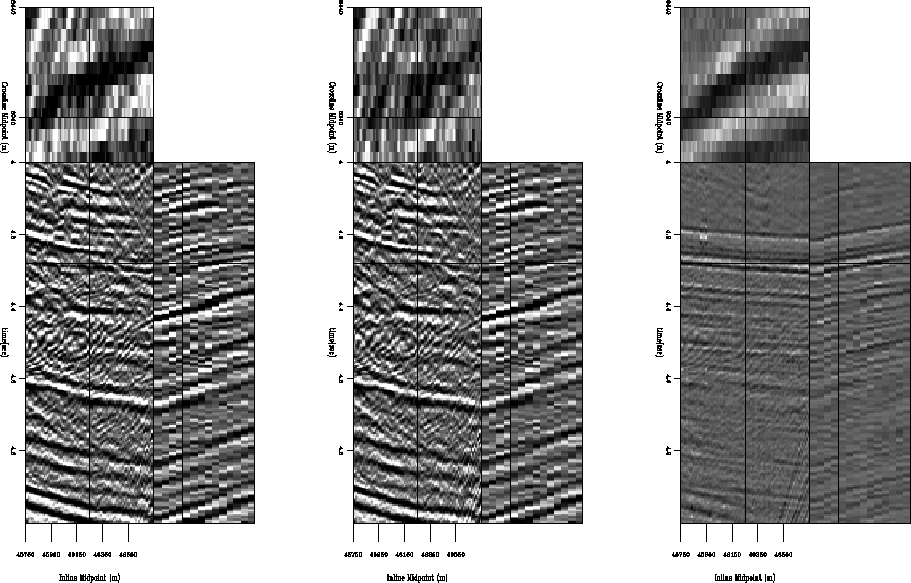
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , a stack of the LSHRTD estimated
primaries, can be compared directly with the LSJIMP result, Figure
, a stack of the LSHRTD estimated
primaries, can be compared directly with the LSJIMP result, Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Like before, the multiples predominantly stack
out, since the moveout separation is so significant. Still, a noticeable amount
of multiple energy has been removed by LSHRTD, perhaps more than by LSJIMP.
However, we immediately see some removed primary energy: for example, the strong
primary near the bottom of the section.
. Like before, the multiples predominantly stack
out, since the moveout separation is so significant. Still, a noticeable amount
of multiple energy has been removed by LSHRTD, perhaps more than by LSJIMP.
However, we immediately see some removed primary energy: for example, the strong
primary near the bottom of the section.
stackcomp3d.radon.zoom.gc3d
Figure 9
NMO/Stack comparison before and after LSHRTD. Compare directly with Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Left: Raw data. Center: LSHRTD estimated
primaries. Right: difference.
. Left: Raw data. Center: LSHRTD estimated
primaries. Right: difference.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: AVO Analysis Before and
Up: Results
Previous: Results
Stanford Exploration Project
5/30/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
Foster and Mosher (1992). While the Hyperbolic Radon transform is a linear
mapping, it is not time-invariant, and thus cannot be implemented efficiently as
a Fourier domain operator. However, a multiple's residual moveout after NMO is
approximately parabolic (quadratic) with offset, so a time-invariant Parabolic
Radon transform is much faster, though not as accurate
Hampson (1986); Kabir and Marfurt (1999).
)
Foster and Mosher (1992). While the Hyperbolic Radon transform is a linear
mapping, it is not time-invariant, and thus cannot be implemented efficiently as
a Fourier domain operator. However, a multiple's residual moveout after NMO is
approximately parabolic (quadratic) with offset, so a time-invariant Parabolic
Radon transform is much faster, though not as accurate
Hampson (1986); Kabir and Marfurt (1999).
![]() as a raw CMP gather,
as a raw CMP gather, ![]() as the linear mapping between radon
transform space and data space,
as the linear mapping between radon
transform space and data space, ![]() as a mute operator that zeroes primary
energy in radon transform space, and
as a mute operator that zeroes primary
energy in radon transform space, and ![]() as the estimated primaries,
then we can express the radon demultiple process in equation form:
as the estimated primaries,
then we can express the radon demultiple process in equation form:
![]() , then applied a mute function which is zero for
velocities greater than 90% known stacking velocity. The mute tapers linearly
from 1.0 to 0.0 between 85% and 90% of the stacking velocity. The
computational cost of LSHRTD is very similar to the cost of applying LSJIMP.
, then applied a mute function which is zero for
velocities greater than 90% known stacking velocity. The mute tapers linearly
from 1.0 to 0.0 between 85% and 90% of the stacking velocity. The
computational cost of LSHRTD is very similar to the cost of applying LSJIMP.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the results of applying LSJIMP and
LSHRTD on a single CMP gather from the CGG 3-D data (CMPx=100, CMPy=4). The
LSHRTD results are quite good, as we expect, given the high velocity gradient
and relatively simple moveout seen in this region of the data. Spatial aliasing
causes some artifacts on the LSHRTD primaries (Figure
compares the results of applying LSJIMP and
LSHRTD on a single CMP gather from the CGG 3-D data (CMPx=100, CMPy=4). The
LSHRTD results are quite good, as we expect, given the high velocity gradient
and relatively simple moveout seen in this region of the data. Spatial aliasing
causes some artifacts on the LSHRTD primaries (Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b)), around
(b)), around ![]() seconds. The radon
primaries seem to contain a bit more spatially uncorrelated noise than the
LSJIMP primaries. LSJIMP is a more ``surgical'' separation technique, although
the model regularization operators also exploit moveout differences to separate
multiples and primaries.
seconds. The radon
primaries seem to contain a bit more spatially uncorrelated noise than the
LSJIMP primaries. LSJIMP is a more ``surgical'' separation technique, although
the model regularization operators also exploit moveout differences to separate
multiples and primaries.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , a stack of the LSHRTD estimated
primaries, can be compared directly with the LSJIMP result, Figure
, a stack of the LSHRTD estimated
primaries, can be compared directly with the LSJIMP result, Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Like before, the multiples predominantly stack
out, since the moveout separation is so significant. Still, a noticeable amount
of multiple energy has been removed by LSHRTD, perhaps more than by LSJIMP.
However, we immediately see some removed primary energy: for example, the strong
primary near the bottom of the section.
. Like before, the multiples predominantly stack
out, since the moveout separation is so significant. Still, a noticeable amount
of multiple energy has been removed by LSHRTD, perhaps more than by LSJIMP.
However, we immediately see some removed primary energy: for example, the strong
primary near the bottom of the section.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Left: Raw data. Center: LSHRTD estimated
primaries. Right: difference.
. Left: Raw data. Center: LSHRTD estimated
primaries. Right: difference.