Image perturbations

A simple way to define the image perturbation ($\Delta \r$)is to take the image obtained with the background slowness and improve it by applying an image enhancement operator. There are many techniques that can be used to obtain an enhanced image.

• One possibility is to flatten events in angle-domain common-image gathers (ADCIG) by using residual moveout.
• Another possibility is to use residual migration to flatten ADCIGs and, at the same time, focus diffractions which can be observed in common-offset sections.

In principle, both focusing in space (along the midpoint axis) and focusing in offset are velocity indicators, and they should be used together to achieve the highest accuracy. In this paper, however, we emphasize migration velocity analysis using only focusing of diffractions along the spatial axes.

In our current implementation, we use prestack Stolt residual migration Sava (2003); Stolt (1996) as the image enhancement operator (${\bf K}$). This residual migration operator applied to the background image creates new images ($\r$), functions of a scalar parameter ($\rho$), which represents the ratio of a new slowness model relative to the background one:  

$$\r = {\bf K}\left(\rho \right)\left[\r_b \right]\;.$$ (8)

We can now take the image perturbation to be the difference between the improved image ($\r$) and the background image ($\r_b$):  

$$\Delta \r= \r - \r_b \;.$$ (9)

The main challenge with this method of constructing image perturbations for WEMVA is that the two images, $\r$ and $\r_b$,can get out of phase, such that they risk violating the requirements of the first-order Born approximation Sava and Biondi (2004a). For example, we might end up subtracting unfocused from focused diffractions at different locations in the image.

We address this challenge by using linearized image perturbations . We run residual migration for a large number of parameters $\rho$ and pick at every location the value where the image is best focused. Then we estimate at every point the gradient of the image relative to the $\rho$ parameter and construct the image perturbations using the following relation:  

$$\Delta \r\approx \left. {\bf K}^{'} \right\vert _{\rho=1} \left[\r_b \right]\Delta \rho \;,$$ (10)

where, by definition, $\Delta \rho = 1-\rho$.

The main benefit of constructing image perturbations with equation (10) is that we avoid the danger of subtracting images that are out of phase. In fact, we do not subtract images at all, but we simply construct the image perturbation that corresponds to a particular map of residual migration parameters ($\rho$). In this way, we honor the information from residual migration, but we are safe relative to the limits of the first-order Born approximation.

Figures 1 and 2 illustrate the migration velocity analysis methodology using residual migration and linearized image perturbations.

 

DIFLAsrm
Figure 1 Residual migration applied to three simple synthetic models (from left to right). From top to bottom, the images correspond to the ratios $\rho=0.7, 0.8, 0.9, 1.0, 1.1$.The middle row corresponds to the correct velocity, when all diffractors are focused.

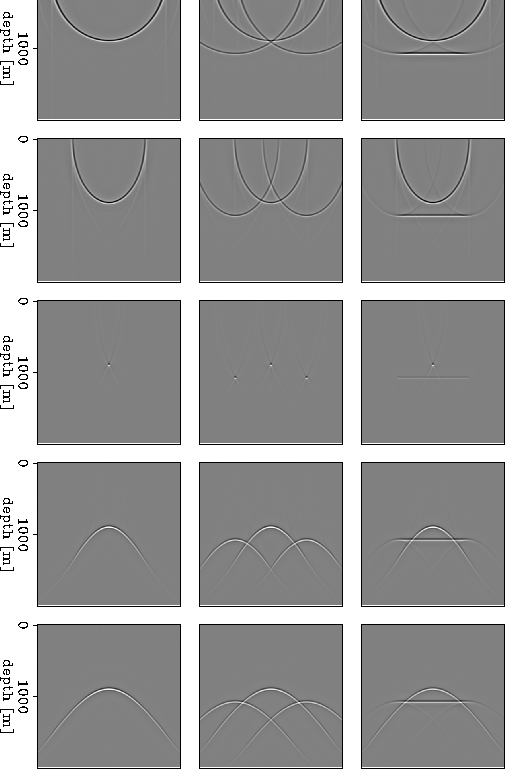Figure 1 shows three simple models with diffractors and reflectors with a constant velocity v=2000 m/s. We use these three models to illustrate different situations: an isolated diffractor at location x=2000 m and depth z=900 m, (Figure 1, left), the same diffractor flanked by other diffractors at z=1100 m (Figure 1, middle), and finally the same diffractor next to a short reflector at z=1100 m (Figure 1, right).

We migrate each synthetic datum with an incorrect velocity, v=1800 m/s, and then run residual migration with various velocity ratios from $\rho=0.7$ to $\rho=1.1$.From top to bottom, each row corresponds to a different velocity ratio as follows: 0.7, 0.8, 0.9, 1.0, 1.1. For all residual migration examples, we have eliminated the vertical shift induced by the different velocities, such that only the diffraction component of residual migration is left. Thus, we can better compare focusing of various events without being distracted by their vertical movement.

The images at $\rho=0.9$ are the best focused images. Since both the backgrounds and the perturbations are constant, the images focus at a single ratio parameter. The ratio difference between the original images at $\rho=1.0$and the best focused images at $\rho=0.9$ is $\Delta \rho=0.1$.In general, the images focus at different ratios at different locations; therefore $\Delta \rho$ is a spatially variable function.

Using the background images and the measured $\Delta \rho$, we compute the linearized image perturbations (Figure 2, top), and using the WEMVA operator we compute the corresponding slowness perturbations after 15 linear iterations (Figure 2, bottom). The image perturbations closely resemble the background image (Figure 1, fourth row from top), with a $\pi/2$ phase shift and appropriate scaling with the measured $\Delta \rho$.

For all models in Figures 1 and 2, we measure focusing on a single event (the main diffractor at x=2000 m and depth z=900 m), but assign the computed $\Delta \rho$ to other elements of the image in the vicinity of this diffractor. The rationale for doing so is that we can assume that all elements at a particular location are influenced by roughly the same part of the model. Therefore, not only is a priori separation of the diffractors from the reflectors not required, but the additional elements present in the image perturbation add robustness to the inversion.

 

DIFLAmva Figure 2 Migration velocity analysis for the three simple synthetic models in Figure 1. The top row depicts image perturbations, and the bottom row depicts slowness perturbations obtained after 15 linear iterations.