




Next: Conclusions
Up: Results
Previous: LSJIMP versus Radon Demultiple
Amplitude-versus-offset or AVO analysis is perhaps the most commonly utilized
direct hydrocarbon indicator in exploration reflection seismology today. The
stacked results before and after LSJIMP on the Green Canyon 3-D dataset showed
that stacking greatly attenuates multiples. However, from the prestack data, we
saw that the multiples are prominent, and would surely inhibit signal processing
techniques, like AVO analysis, if left intact. In this section, I illustrate
how LSJIMP improves the AVO analysis of the Green Canyon 3-D data.
Shuey (1985) showed that in a 1-D earth, the measured reflection
strength of an event at the surface is approximately linear with the square of
its incidence angle, at angles less than 30 degrees. In a 1-D earth, the NMO
equation gives an approximate relationship between offset and incidence angle.
Claerbout (1995) defines the ``stepout'', p, as the spatial
derivative of an event's traveltime curve:
| 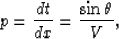 |
(9) |
where 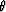 is the incidence angle and V is the velocity at the surface; in
the marine case, simply water velocity. In a 1-D earth, the traveltime curve of
a primary reflection is approximately given by the NMO equation. Taking its
derivative with respect to offset, then substituting into equation
(9) gives the following expression for the sine of incidence angle
as a function of offset:
is the incidence angle and V is the velocity at the surface; in
the marine case, simply water velocity. In a 1-D earth, the traveltime curve of
a primary reflection is approximately given by the NMO equation. Taking its
derivative with respect to offset, then substituting into equation
(9) gives the following expression for the sine of incidence angle
as a function of offset:
| 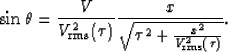 |
(10) |
Reflection data as a function of offset may be mapped to 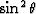 via
equation (10), at which point the AVO ``slope'' and ``intercept''
parameters may be estimated, usually via a linear least-squares fit to the
data after resampling from offset to
via
equation (10), at which point the AVO ``slope'' and ``intercept''
parameters may be estimated, usually via a linear least-squares fit to the
data after resampling from offset to 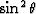 .
.
Figure 12 illustrates the estimation of AVO slope and
intercept parameters on a deep reflector in the Green Canyon 3-D data, before
and after application of LSJIMP. The reflector, which is well under the
multiples in the data, is denoted on the zero offset section with ``O'' symbols.
The maximum amplitude in a small time window around the reflection were picked
automatically, and make up the input data to the least-squares estimation.
maxampl.gc3d.4-5
Figure 12
AVO parameter estimation for a deep reflector. Left: zero offset section,
``O'' symbols denote reflector of interest. Right, top: AVO intercept
parameter before and after LSJIMP, as a function of midpoint. Right, bottom:
AVO slope parameter before and after LSJIMP, as a function of midpoint.

We see that while the parameter estimates contain the same trends before and
after LSJIMP, the LSJIMP result is more consistent and less ``noisy'' across
midpoint. My implementation of LSJIMP works on a CMP-by-CMP basis, so the
results shown in Figure 12 are not smoothed across
midpoint. The similarity across midpoint is an expression of the true lithology
- lithology which LSJIMP better reveals.
Figure 13 illustrates, as a function of midpoint, the
small time windows taken around the deep reflector shown in Figure
12, before and after LSJIMP. The input data to an AVO
parameter estimation are picked maximum amplitudes within the time window as a
function of 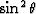 . Notice the significant increase in reflector
clarity after LSJIMP. Also recall that the data residuals (e.g., in Figures
8 and 9)
are quite small. Therefore, the cleaner reflection events after LSJIMP in
Figure 13 are not only better for AVO analysis - they
also fit the recorded data in a quantitative fashion. LSJIMP is not an ad
hoc post-processing technique.
. Notice the significant increase in reflector
clarity after LSJIMP. Also recall that the data residuals (e.g., in Figures
8 and 9)
are quite small. Therefore, the cleaner reflection events after LSJIMP in
Figure 13 are not only better for AVO analysis - they
also fit the recorded data in a quantitative fashion. LSJIMP is not an ad
hoc post-processing technique.
avogather.gc3d.4-5
Figure 13
Small time windows around the deep reflector shown in Figure
12, before and after LSJIMP. Individual panels along
the vertical axis correspond to windows taken at different midpoint locations.
Left: Data windows before LSJIMP. Right: Data windows after LSJIMP.






Next: Conclusions
Up: Results
Previous: LSJIMP versus Radon Demultiple
Stanford Exploration Project
5/23/2004
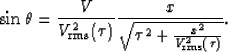
![]() . Notice the significant increase in reflector
clarity after LSJIMP. Also recall that the data residuals (e.g., in Figures
8 and 9)
are quite small. Therefore, the cleaner reflection events after LSJIMP in
Figure 13 are not only better for AVO analysis - they
also fit the recorded data in a quantitative fashion. LSJIMP is not an ad
hoc post-processing technique.
. Notice the significant increase in reflector
clarity after LSJIMP. Also recall that the data residuals (e.g., in Figures
8 and 9)
are quite small. Therefore, the cleaner reflection events after LSJIMP in
Figure 13 are not only better for AVO analysis - they
also fit the recorded data in a quantitative fashion. LSJIMP is not an ad
hoc post-processing technique.
