




Next: 3-D Theory
Up: Brown: 3-D LSJIMP
Previous: Introduction
LSJIMP models the recorded data as the sum of primary reflections and p orders
of pegleg multiples from 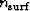 multiple generators. An
multiple generators. An
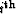 -order pegleg splits into i+1 legs. Denoting the primaries
-order pegleg splits into i+1 legs. Denoting the primaries
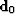 and the
and the 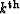 leg of the
leg of the 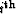 order pegleg from the
order pegleg from the
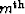 multiple generator
multiple generator 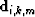 , the modeled data takes the
following form:
, the modeled data takes the
following form:
| 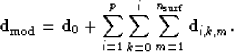 |
(1) |
If we have designed imaging operators that map primaries and multiples to
comparable signal events (kinematics and angle-dependent amplitudes), we can
write the 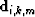 as linear functions of prestack images. We can
similarly denote the modeling operators (adjoint to imaging) for primaries and
peglegs as
as linear functions of prestack images. We can
similarly denote the modeling operators (adjoint to imaging) for primaries and
peglegs as 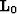 and
and 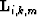 , respectively, and the images of the
primaries and peglegs as
, respectively, and the images of the
primaries and peglegs as 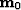 and
and 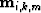 , respectively.
Rewriting equation (1), we have:
, respectively.
Rewriting equation (1), we have:
| 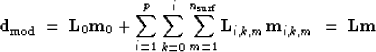 |
(2) |
The LSJIMP method optimizes the primary and multiple images, 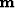 , by
minimizing the
, by
minimizing the 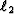 norm of the difference between the recorded data,
norm of the difference between the recorded data,
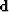 , and the modeled data,
, and the modeled data, 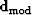 :
:
| 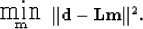 |
(3) |
Minimization (3) is under-determined for most choices of
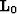 and
and 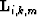 , implying infinitely many solutions. Crosstalk
leakage is a symptom of the problem. For instance,
, implying infinitely many solutions. Crosstalk
leakage is a symptom of the problem. For instance, 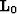 maps residual
first-order multiple energy in
maps residual
first-order multiple energy in 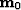 to the position of a first-order
multiple in data space. Minimization (3) alone cannot
distinguish between crosstalk and signal. Without model regularization, the
basic LSJIMP problem is intractable.
to the position of a first-order
multiple in data space. Minimization (3) alone cannot
distinguish between crosstalk and signal. Without model regularization, the
basic LSJIMP problem is intractable.
Previously Brown (2003b), I devised discriminants between
crosstalk and signal, and used them to derive three model regularization operators
which choose the set of primary and multiple images which are optimally free of
crosstalk. Moreover, these operators exploit signal multiplicity-within and
between images-to increase signal fidelity, fill coverage gaps, and combine
multiple and primary information. These model regularization operators are the
key to the LSJIMP method's novelty.
To solve the regularized LSJIMP problem, we supplement minimization
(3) with the three model regularization operators:
| ![\begin{displaymath}
\mbox{ \raisebox{-1.0ex}{ $\stackrel{\textstyle \mbox{\LARGE...
...]} \Vert^2
\; + \; \epsilon_3^2 \Vert \bold r_m^{[3]} \Vert^2.\end{displaymath}](img18.gif) |
(4) |
![$\bold r_m^{[1]}$](img19.gif) ,
, ![$\bold r_m^{[2]}$](img20.gif) , and
, and ![$\bold r_m^{[3]}$](img21.gif) are the model
residuals corresponding to differencing across images, differencing across offset,
and crosstalk penalty weighting, respectively. Scalars
are the model
residuals corresponding to differencing across images, differencing across offset,
and crosstalk penalty weighting, respectively. Scalars 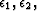 and
and 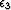 balance the relative weight of the three model residuals with
the data residual. I use the conjugate gradient method for minimization
(4).
balance the relative weight of the three model residuals with
the data residual. I use the conjugate gradient method for minimization
(4).
Previously Brown (2003a,c), I outlined an
efficient prestack, true relative amplitude imaging scheme for pegleg multiples.
We can rewrite 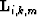 as the cascade of a differential geometric
spreading correction for multiples (
as the cascade of a differential geometric
spreading correction for multiples (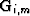 ), Snell Resampling to
normalize a multiple's AVO to its primary (
), Snell Resampling to
normalize a multiple's AVO to its primary (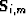 ), HEMNO
(Heterogeneous Earth Multiple NMO Operator) to kinematically image split peglegs
(
), HEMNO
(Heterogeneous Earth Multiple NMO Operator) to kinematically image split peglegs
(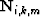 ), and finally, application of the multiple generator's
spatially-variant reflection coefficient (
), and finally, application of the multiple generator's
spatially-variant reflection coefficient (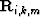 ):
):
| 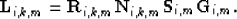 |
(5) |
The imaging operator for primaries, 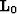 , is simply NMO. The imaged
multiples and primaries on the
, is simply NMO. The imaged
multiples and primaries on the 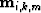 in equation
(2) are directly comparable in terms of kinematics and
amplitudes. We can exploit this important fact (with model regularization) to
discriminate crosstalk from signal, and also to spread information between the
images. A true relative amplitude imaging scheme like equation
(5) is crucial to fully leverage the multiples in this
joint imaging algorithm. Since we apply the operator and its adjoint many times
in iterative optimization, computational efficiency is crucial. Because HEMNO
images (like NMO) by vertical stretch, equation (5) is
fast, memory-conserving, and robust to poorly sampled wavefields, which are the
norm with 3-D acquisition. Brown and Guitton (2004) demonstrated that this
modeling/imaging approach can accurately model multiples, even in a moderately
complex earth.
in equation
(2) are directly comparable in terms of kinematics and
amplitudes. We can exploit this important fact (with model regularization) to
discriminate crosstalk from signal, and also to spread information between the
images. A true relative amplitude imaging scheme like equation
(5) is crucial to fully leverage the multiples in this
joint imaging algorithm. Since we apply the operator and its adjoint many times
in iterative optimization, computational efficiency is crucial. Because HEMNO
images (like NMO) by vertical stretch, equation (5) is
fast, memory-conserving, and robust to poorly sampled wavefields, which are the
norm with 3-D acquisition. Brown and Guitton (2004) demonstrated that this
modeling/imaging approach can accurately model multiples, even in a moderately
complex earth.





Next: 3-D Theory
Up: Brown: 3-D LSJIMP
Previous: Introduction
Stanford Exploration Project
5/23/2004
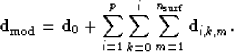
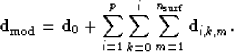
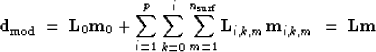
![]() as the cascade of a differential geometric
spreading correction for multiples (
as the cascade of a differential geometric
spreading correction for multiples (![]() ), Snell Resampling to
normalize a multiple's AVO to its primary (
), Snell Resampling to
normalize a multiple's AVO to its primary (![]() ), HEMNO
(Heterogeneous Earth Multiple NMO Operator) to kinematically image split peglegs
(
), HEMNO
(Heterogeneous Earth Multiple NMO Operator) to kinematically image split peglegs
(![]() ), and finally, application of the multiple generator's
spatially-variant reflection coefficient (
), and finally, application of the multiple generator's
spatially-variant reflection coefficient (![]() ):
):