




Next: CGG with iteratively reweighted
Up: Conjugate Guided Gradient(CGG) method
Previous: CGG with iteratively reweighted
Another way to modify the gradient direction
is to modify the gradient vector after the gradient is computed
from a given residual.
Since the gradient vector is in the model space,
any modification of the gradient vector imposes
some constraint in the model space.
If we know some characteristics of the solution
which can be expressed in terms of weighting in the solution space,
we can use that a priori knowledge to redirect
the gradient vector by applying a weight to it.
This algorithm can be implemented as follows:
 iterate {
iterate {
![$\bold W \quad\longleftarrow\quad{\bf diag}[f(\bold m)]$](img40.gif)
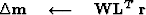
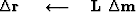
 } .
} .
Even though weighting the gradient has
different meaning from weighting the residual,
the analysis is similar in both cases.
As we redefined the contribution of each residual element
by weighting it with the absolute value
of itself to some power:
we can do the same with each model element
in the solution,
| 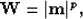 |
(9) |
where p is a real number that depends on the problem we wish to.
When we have a finite model space
we are applying a uniform weight
to the finite model space and zero weight
to the outlying space.
If the operator used in the inversion is close to unitary,
the solution obtained after the first iteration already
closely approximates the real solution.
Therefore, weighting the gradient
with some power of the absolute value of the previous
iteration means that we down-weight the importance of small model values
and improve the fit to the data by emphasizing model components
that already have large values.





Next: CGG with iteratively reweighted
Up: Conjugate Guided Gradient(CGG) method
Previous: CGG with iteratively reweighted
Stanford Exploration Project
5/23/2004
iterate {
![$\bold W \quad\longleftarrow\quad{\bf diag}[f(\bold m)]$](img40.gif)
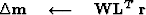
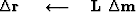
} .