




Next: Thomsen's
Up: THOMSEN PARAMETERS AND
Previous: THOMSEN PARAMETERS AND
An important anisotropy parameter for quasi-SV-waves (which is our
main interest in this paper) is Thomsen's parameter
 , defined in equation (2).
Formula (12) for a may be rewritten as
, defined in equation (2).
Formula (12) for a may be rewritten as
| 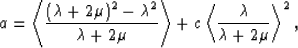 |
(14) |
which can be rearranged into the convenient and illuminating form
| ![\begin{eqnarray}
a = \left<\lambda+2\mu\right\gt -
c\left[\left<{{\lambda^2}\ove...
...ight\gt
-\left<{{\lambda}\over{\lambda+2\mu}}\right\gt^2\right].
\end{eqnarray}](img38.gif) |
(15) |
This formula is very instructive because the term in square brackets
is in Cauchy-Schwartz form
[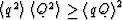 ], so this factor is nonnegative. Furthermore,
the magnitude of this term depends
mainly on the fluctuations in the
], so this factor is nonnegative. Furthermore,
the magnitude of this term depends
mainly on the fluctuations in the 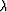 Lamé
parameter, and is largely independent of
Lamé
parameter, and is largely independent of 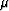 , since
, since
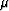 appears only in the weighting factor
appears only in the weighting factor 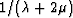 .Clearly, if
.Clearly, if 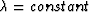 , then this bracketed factor
vanishes identically, regardless of the behavior of
, then this bracketed factor
vanishes identically, regardless of the behavior of
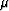 . Large fluctuations in
. Large fluctuations in 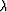 will tend to make this term large.
If in addition we consider Thomsen's parameter
will tend to make this term large.
If in addition we consider Thomsen's parameter  written in a
similar fashion as
written in a
similar fashion as
| ![\begin{eqnarray}
2\epsilon =
\left[\left<\lambda+2\mu\right\gt\left<{{1}\over{\l...
...ight\gt
-\left<{{\lambda}\over{\lambda+2\mu}}\right\gt^2\right],
\end{eqnarray}](img42.gif) |
(16) |
we find that the term enclosed in the first bracket on the right hand
side is again in Cauchy-Schwartz form showing that it always makes a positive
contribution unless 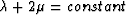 , in which case it vanishes.
Similarly, the term enclosed in the second set of brackets is always
non-negative, but the minus preceding the second bracket causes
this contribution to make a negative contribution to
, in which case it vanishes.
Similarly, the term enclosed in the second set of brackets is always
non-negative, but the minus preceding the second bracket causes
this contribution to make a negative contribution to 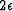 unless
unless 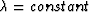 , in which case it vanishes.
So, in general the sign of
, in which case it vanishes.
So, in general the sign of  is indeterminate.
The Thomsen parameter
is indeterminate.
The Thomsen parameter  may have either a positive or a
negative sign for a TI medium composed of arbitrary thin isotropic layers.
Thomsen (2002) states that
may have either a positive or a
negative sign for a TI medium composed of arbitrary thin isotropic layers.
Thomsen (2002) states that 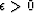 if K and
if K and 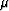 are
positively correlated. But (16) shows that such correlations
only produce
are
positively correlated. But (16) shows that such correlations
only produce 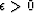 with certainty if they are also
supplemented by the stronger condition that
with certainty if they are also
supplemented by the stronger condition that 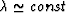 [in fact,
[in fact, 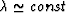 implies that there is a positive correlation
between K and
implies that there is a positive correlation
between K and 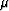 , but the reverse does not necessarily hold
unless we also assume that the fluctuations in
, but the reverse does not necessarily hold
unless we also assume that the fluctuations in 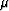 are quite small --
an assumption that we do not make here].
are quite small --
an assumption that we do not make here].
Fluctuations of 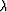 in the earth have important implications
for oil and gas exploration. As we
recalled in our earlier discussion, Gassmann's well-known results
(Gassmann, 1951) show that, when isotropic porous elastic media are saturated
with any fluid, the fluid has no mechanical effect on the shear
modulus
in the earth have important implications
for oil and gas exploration. As we
recalled in our earlier discussion, Gassmann's well-known results
(Gassmann, 1951) show that, when isotropic porous elastic media are saturated
with any fluid, the fluid has no mechanical effect on the shear
modulus 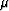 , but -- when these results apply --
it can have a significant effect on the bulk modulus
, but -- when these results apply --
it can have a significant effect on the bulk modulus
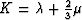 , and therefore on
, and therefore on 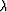 . Thus, observed
(high spatial frequency) variations in layer shear modulus
. Thus, observed
(high spatial frequency) variations in layer shear modulus
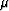 should have no direct information about fluid content,
while such variations observed in layer Lamé parameter
should have no direct information about fluid content,
while such variations observed in layer Lamé parameter
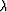 , especially if they are large variations,
may contain important clues about variations in fluid content.
So the observed structure of
, especially if they are large variations,
may contain important clues about variations in fluid content.
So the observed structure of  in (16)
strongly suggests that small positive and all negative values of
in (16)
strongly suggests that small positive and all negative values of
 may be important indicators of significant fluctuations
in fluid content (Berryman et al., 1999).
may be important indicators of significant fluctuations
in fluid content (Berryman et al., 1999).





Next: Thomsen's
Up: THOMSEN PARAMETERS AND
Previous: THOMSEN PARAMETERS AND
Stanford Exploration Project
5/23/2004
![]() , defined in equation (2).
Formula (12) for a may be rewritten as
, defined in equation (2).
Formula (12) for a may be rewritten as
![]() in the earth have important implications
for oil and gas exploration. As we
recalled in our earlier discussion, Gassmann's well-known results
(Gassmann, 1951) show that, when isotropic porous elastic media are saturated
with any fluid, the fluid has no mechanical effect on the shear
modulus
in the earth have important implications
for oil and gas exploration. As we
recalled in our earlier discussion, Gassmann's well-known results
(Gassmann, 1951) show that, when isotropic porous elastic media are saturated
with any fluid, the fluid has no mechanical effect on the shear
modulus ![]() , but -- when these results apply --
it can have a significant effect on the bulk modulus
, but -- when these results apply --
it can have a significant effect on the bulk modulus
![]() , and therefore on
, and therefore on ![]() . Thus, observed
(high spatial frequency) variations in layer shear modulus
. Thus, observed
(high spatial frequency) variations in layer shear modulus
![]() should have no direct information about fluid content,
while such variations observed in layer Lamé parameter
should have no direct information about fluid content,
while such variations observed in layer Lamé parameter
![]() , especially if they are large variations,
may contain important clues about variations in fluid content.
So the observed structure of
, especially if they are large variations,
may contain important clues about variations in fluid content.
So the observed structure of ![]() in (16)
strongly suggests that small positive and all negative values of
in (16)
strongly suggests that small positive and all negative values of
![]() may be important indicators of significant fluctuations
in fluid content (Berryman et al., 1999).
may be important indicators of significant fluctuations
in fluid content (Berryman et al., 1999).