




Next: Gassmann results for isotropic
Up: NOTATION AND SOME PRIOR
Previous: NOTATION AND SOME PRIOR
We begin by introducing some notation needed in the remainder of the paper.
For transversely isotropic media with vertical symmetry axis,
the relationship between components of stress 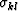 and strain
and strain
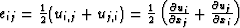 (where uj is the
jth component of the displacement vector) is given by
(where uj is the
jth component of the displacement vector) is given by
| 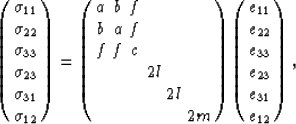 |
(1) |
where a = b + 2m (e.g., Musgrave, 1970; Auld, 1973),
with i,j,k,l each ranging from 1 to 3 in Cartesian coordinates.
The matrix describes isotropic media in the special case when
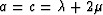 ,
, 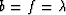 , and
, and 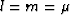 .
.
The Thomsen (1986) parameters  ,
, 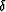 , and
, and 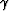 are related
to these stiffnesses by
are related
to these stiffnesses by
| 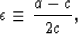 |
(2) |
| 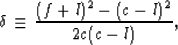 |
(3) |
| 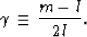 |
(4) |
Certain interpretations are allowed for these parameters when they are
small enough. For P-wave propagation in the earth near the vertical,
the important anisotropy parameter is 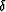 . For SV-wave
propagation near the vertical, the combination
. For SV-wave
propagation near the vertical, the combination
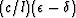 plays essentially the
same role as
plays essentially the
same role as 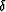 does for P-waves. For SH-waves, the pertinent
anisotropy parameter is
does for P-waves. For SH-waves, the pertinent
anisotropy parameter is 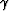 . All three of the Thomsen parameters
vanish for an isotropic medium, and the interpretations mentioned are
valid for weakly anisotropic media such that all these parameters are
relatively small (< 1). However, the definitions are also useful
outside the range of these constraints, and we will use the same definitions (and
also continue to call them the ``Thomsen parameters'') even when the smallness
condition is violated; there is no fundamental problem doing this
as long as it is recognized that the interpretations already mentioned
in this paragraph are not necessarily valid any more when the
parameters are large. This generalization of the Thomsen parameters
will however require us to be careful in our subsequent usage of the
parameters, as they cannot always be assumed to be small here as is
usual in other treatments. Unless explicitly stated otherwise, the
parameters
. All three of the Thomsen parameters
vanish for an isotropic medium, and the interpretations mentioned are
valid for weakly anisotropic media such that all these parameters are
relatively small (< 1). However, the definitions are also useful
outside the range of these constraints, and we will use the same definitions (and
also continue to call them the ``Thomsen parameters'') even when the smallness
condition is violated; there is no fundamental problem doing this
as long as it is recognized that the interpretations already mentioned
in this paragraph are not necessarily valid any more when the
parameters are large. This generalization of the Thomsen parameters
will however require us to be careful in our subsequent usage of the
parameters, as they cannot always be assumed to be small here as is
usual in other treatments. Unless explicitly stated otherwise, the
parameters  ,
, 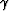 , and
, and 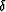 are not small quantities
in this paper.
are not small quantities
in this paper.
It is also useful to note for later reference that
| 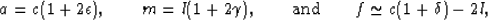 |
(5) |
where smallness of 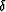 was in fact assumed in the third expression.
In TI media, c and l are directly related to the velocities normal
to the layering. Then,
was in fact assumed in the third expression.
In TI media, c and l are directly related to the velocities normal
to the layering. Then,  ,
, 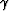 , and
, and 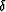 measure
the deviations from these normal velocities at other angles. We
present the relevant details of the phase velocity analysis later
in the paper.
measure
the deviations from these normal velocities at other angles. We
present the relevant details of the phase velocity analysis later
in the paper.





Next: Gassmann results for isotropic
Up: NOTATION AND SOME PRIOR
Previous: NOTATION AND SOME PRIOR
Stanford Exploration Project
5/23/2004
![]() and strain
and strain
![]() (where uj is the
jth component of the displacement vector) is given by
(where uj is the
jth component of the displacement vector) is given by
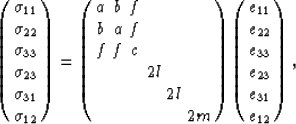
![]() ,
, ![]() , and
, and ![]() are related
to these stiffnesses by
are related
to these stiffnesses by