




Next: Interpretation of the results
Up: INTERPRETATION OF P AND
Previous: General analysis for VTI
The analysis presented in the previous subsection
is general for all VTI elastic media.
But we can say more by assuming now that the anisotropy arises due to
layers of isotropic elastic (or possibly poroelastic) media.
Then, using (8)-(12), we have the following relations
| 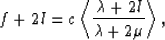 |
(51) |
| 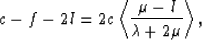 |
(52) |
and
| ![\begin{eqnarray}
a - f - 2l = 2c \left\{\left<{{2m-\mu -l}\over{\lambda + 2\mu}}...
...
- \left<{{\mu}\over{\lambda + 2\mu}}\right\gt^2\right]\right\}.
\end{eqnarray}](img112.gif) |
(53) |
Eq. (51) is an easy consequence of the Backus averaging
formulas.
Then, (52) shows that c differs from f + 2l only by a
term that measures the difference in the weighted average of 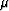 and
l. Eq. (53) shows that a differs from f + 2l
in a more complicated fashion that depends on the difference in the
weighted average of (2m-l) and
and
l. Eq. (53) shows that a differs from f + 2l
in a more complicated fashion that depends on the difference in the
weighted average of (2m-l) and 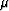 , as well as a term that is
higher order in the fluctuations of the layer
, as well as a term that is
higher order in the fluctuations of the layer 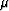 values.
Combining these results, we have
values.
Combining these results, we have
| ![\begin{eqnarray}
G_{eff} = m - {{4c}\over{3}}\left[\left<{{\mu^2}\over{\lambda +...
...right\gt
- \left<{{\mu}\over{\lambda + 2\mu}}\right\gt^2\right],
\end{eqnarray}](img113.gif) |
(54) |
showing that all the interesting behavior (including strong 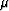 fluctuations in the layers together with
fluctuations in the layers together with 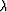 dependence) is
collected in Geff.
Since the product of (52) and (53) is clearly of
higher order in the fluctuations of the layer shear moduli, it is not
hard to see that, to leading order when these fluctuation effects are small,
dependence) is
collected in Geff.
Since the product of (52) and (53) is clearly of
higher order in the fluctuations of the layer shear moduli, it is not
hard to see that, to leading order when these fluctuation effects are small,
| 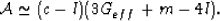 |
(55) |
To give a quick estimate, note that if all the layers have the same
value of Poisson's ratio, then the ratio 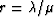 is
constant. Then, it is easy to show that Geff = m - 4(m-l)/3(2+r).
Since
is
constant. Then, it is easy to show that Geff = m - 4(m-l)/3(2+r).
Since 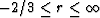 , the effective shear modulus
for this class of models lies in the range
, the effective shear modulus
for this class of models lies in the range 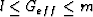 .From this fact, we can conclude that the important coefficient in
(40) is given to a good approximation by
.From this fact, we can conclude that the important coefficient in
(40) is given to a good approximation by
| 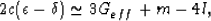 |
(56) |
and ranges from 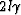 to
to 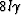 .
.
To study the fluid effects, the drained Lamé parameter 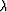 in
each layer should be replaced under undrained conditions by
in
each layer should be replaced under undrained conditions by
| 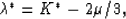 |
(57) |
where K* was defined by (6). Then, for small
fluctuations in 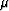 , Eq. (56) shows that the
leading order terms due to these shear modulus variations contributing
to
, Eq. (56) shows that the
leading order terms due to these shear modulus variations contributing
to 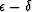 actually do not depend on the fluids at all
(since m-l does not depend on them). With no fluid in the pores,
there is a contribution to the shear wave speed for SV in layered
media, just due to the fluctuations in the shear moduli. One part
of the contribution is always independent of any fluids that might be
present, but the magnitude of this contribution (which is always
positive) is small whenever the difference m-l is also small. If
m-l is large, then the magnitude of the additional increase due to liquids
in the pores can be very substantial as we will see in the following examples.
So the effects of liquids on Geff will generally be weak when the
fluctuations in
actually do not depend on the fluids at all
(since m-l does not depend on them). With no fluid in the pores,
there is a contribution to the shear wave speed for SV in layered
media, just due to the fluctuations in the shear moduli. One part
of the contribution is always independent of any fluids that might be
present, but the magnitude of this contribution (which is always
positive) is small whenever the difference m-l is also small. If
m-l is large, then the magnitude of the additional increase due to liquids
in the pores can be very substantial as we will see in the following examples.
So the effects of liquids on Geff will generally be weak when the
fluctuations in 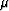 are weak, and strong when they are strong.
are weak, and strong when they are strong.
Furthermore, when the product 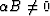 ,we first choose to define
,we first choose to define
| 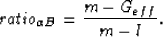 |
(58) |
so that, for all possible layered models, we have
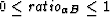 . Then, we consider plotting
the quantity
. Then, we consider plotting
the quantity 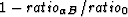 versus
versus
 (which we treat as a simple quantitative measure of the
fluctuations in the layer shear moduli).
To generate a class of 900 models for each of three choices of
(which we treat as a simple quantitative measure of the
fluctuations in the layer shear moduli).
To generate a class of 900 models for each of three choices of
 (treated as a single constant for all layers in each individual
model) in order to illustrate the behavior of these quantities,
I made use of a code of V. Grechka [used previously in a joint
publication (Berryman et al., 1999)]. This code chooses
layer parameters randomly from within the following (arguable,
but generally reasonable) range of values:
(treated as a single constant for all layers in each individual
model) in order to illustrate the behavior of these quantities,
I made use of a code of V. Grechka [used previously in a joint
publication (Berryman et al., 1999)]. This code chooses
layer parameters randomly from within the following (arguable,
but generally reasonable) range of values:
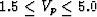 km/s,
km/s,
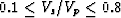 , and
, and
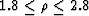
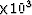 kg/m3.
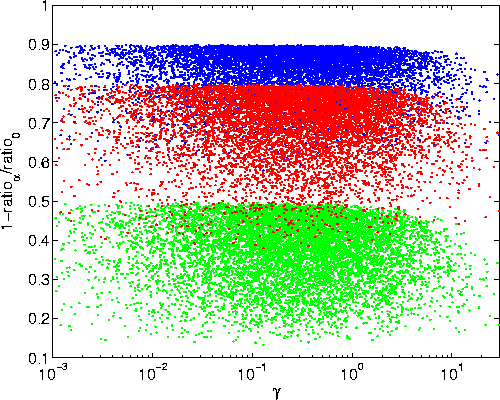
The results are displayed in Figure 1 for
kg/m3.
The results are displayed in Figure 1 for 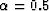 , 0.8, and
0.9. We find empirically that (for B = 1)
the values never exceed
, 0.8, and
0.9. We find empirically that (for B = 1)
the values never exceed  for any set of choices for the
layer model parameters. This apparent fact (as determined by these
computer experiments) does not appear to be easy to
prove from the general formula. But one simple though nontrivial
calculation we can do is based again on an assumption that the
bulk moduli in the layers are always proportional to the shear modulus,
so
for any set of choices for the
layer model parameters. This apparent fact (as determined by these
computer experiments) does not appear to be easy to
prove from the general formula. But one simple though nontrivial
calculation we can do is based again on an assumption that the
bulk moduli in the layers are always proportional to the shear modulus,
so 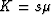 , for some fixed value of of the proportinality factor
s > 0. Then, for a given model, we find that
, for some fixed value of of the proportinality factor
s > 0. Then, for a given model, we find that
| 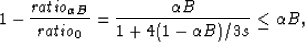 |
(59) |
in agreement with the empiricial result from the synthetic data
shown in Figure 1.
scatter
Figure 1 Scatter plot illustrating how
Geff varies over a
physically sensible range of layered isotropic media
(see text for details) with 2700 distinct models and B = 1
[see Eq. (58) in the text for the definition of 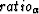 ].
Blue dots are for
].
Blue dots are for 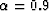 , red for
, red for 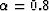 ,and green for
,and green for 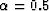 . Note, that in each case,
all the points for a particular choice of
. Note, that in each case,
all the points for a particular choice of  are
bounded above precisely by the value of
are
bounded above precisely by the value of  .(A general proof of this empirical observation is currently lacking.)
.(A general proof of this empirical observation is currently lacking.)

To check the corresponding result for P-waves, we need to estimate 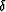 .Making use of (50), we have
.Making use of (50), we have
| ![\begin{eqnarray}
c\delta = -2c\left<{{\mu - l}\over{\lambda + 2\mu}}\right\gt
\l...
...ight\gt^{-1}
\left<{{\mu-l}\over{\lambda+2\mu}}\right\gt\right].
\end{eqnarray}](img136.gif) |
(60) |
Working to the same order as we did for the final expression in
(56), we can neglect the second term in the
square brackets of (60).
What remains shows that pore fluids would have an effect on this
result. The result is
| 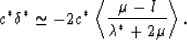 |
(61) |
If desired, a similar replacement can also be made for Geff
in (44) using the fact that 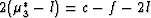 .
Eq. (61) shows that, since c* and
.
Eq. (61) shows that, since c* and 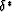 both depend on the
both depend on the  's (although in opposite ways, since
one increases while the other decreases as
's (although in opposite ways, since
one increases while the other decreases as 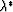 increases),
the product of these factors will have some dependence on fluids.
The degree to which fluctuations in
increases),
the product of these factors will have some dependence on fluids.
The degree to which fluctuations in 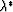 and
and 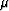 are
correlated, or anticorrelated, as they vary from layer to layer
will also affect these results in predictable ways.
are
correlated, or anticorrelated, as they vary from layer to layer
will also affect these results in predictable ways.





Next: Interpretation of the results
Up: INTERPRETATION OF P AND
Previous: General analysis for VTI
Stanford Exploration Project
5/23/2004
![]() in
each layer should be replaced under undrained conditions by
in
each layer should be replaced under undrained conditions by
![]() ,we first choose to define
,we first choose to define
![]() .Making use of (50), we have
.Making use of (50), we have