




Next: Shot-profile wavefield continuation
Up: Theory
Previous: Theory
Modeling a GPR experiment is a complicated process that, for complete
accuracy, requires taking into account such effects as antenna
radiation patterns and the vectorial nature of electromagnetic (EM)
wave propagation and scattering van der Kruk et al. (2003). It is well known,
however, that seismic processing techniques based on a scalar wave
equation can often be applied very successfully to GPR data
Fisher et al. (1992b). This latter point is not mere coincidence. In many
situations, isotropic scattering and scalar wave propagation
effectively model the kinematics of a GPR experiment. Here, in
applying an imaging algorithm based on a scalar wave equation to GPR
data, we argue that radar propagation kinematics are well
represented. In addition, we suggest that with further development,
effects such as antenna radiation patterns and realistic scattering
could be accounted for in the source and receiver wavefields and
imaging condition.
Considering a situation where Maxwell's equations can be represented
by a 2-D scalar wave equation involves making two approximations.
First, we implicitly assume that the subsurface geology and sources
are strictly 2-D. This results in the decoupled transverse electric
(TE) and transverse magnetic (TM) propagation modes Jackson (1975).
Choosing the TE-mode, we next assume that heterogeneities within the
earth are small such that the gradients of EM constitutive parameters
can be neglected Sena et al. (2003). The result is a scalar wave equation for
transverse electric field, E, which in the frequency (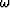 )domain is given by,
)domain is given by,
| ![\begin{displaymath}
\left[ \frac{\partial^2}{\partial z^2}+\frac{\partial^2}{\partial
x^2}\right] E + \omega^2 s^2 E = 0,\end{displaymath}](img2.gif) |
(1) |
where the slowness of wave propagation (i.e. inverse of velocity),
s, is dependent on the medium's dielectric permittivity,  ,and conductivity,
,and conductivity,  , through,
, through,
| 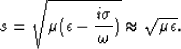 |
(2) |
The magnetic permeability of the medium, 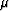 , is roughly
constant for most material likely to be encountered in a routine
radar application. Hence, in low conductivity media (i.e.
, is roughly
constant for most material likely to be encountered in a routine
radar application. Hence, in low conductivity media (i.e. 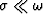 ), the slowness of wavefield propagation is directly
proportional to the dielectric permittivity.
), the slowness of wavefield propagation is directly
proportional to the dielectric permittivity.





Next: Shot-profile wavefield continuation
Up: Theory
Previous: Theory
Stanford Exploration Project
5/23/2004
![]() )domain is given by,
)domain is given by,