Phase-ray extrapolation examples

In this section we illustrate the utility of adaptive phase-ray wavefield extrapolation using 2-D synthetic examples involving progressively more complex velocity models. Underlying ray-coordinate systems were calculated according to equation (12), and wavefields were extrapolated on the computed rayfields using the ray-coordinate 15 equation (equation (9)). All images were computed using uniform time steps with individual $\Delta \t$ dependent on velocity model complexity. Orthogonal coordinate $\gamma$ was parameterized as either a punctual or a plane wave source. Point source images required a parameterization of $\gamma$ over shooting angle starting at radius, R. The initial 4-step coordinate mesh was created from a circularly expanding rayfront with an angular range bounded by $\gamma_{min}$ and $\gamma_{max}$. Initial wavefields consisted of constant amplitude lines separated in $\t$ and distributed uniformly over coordinate $\gamma$. Plane-wave images required a parameterization of $\gamma$ over surface coordinate x_o. The initial 4-step coordinate system was a Cartesian mesh tilted at the dip angle of the plane-wave being extrapolated. Initial wavefields again consisted of constant amplitude lines separated in $\t$ and distributed uniformly over surface position, x_o.

We designed the first extrapolation example to test the method on a smooth velocity function of sufficient contrast to enable overturning waves. The velocity model, shown in the left panel of Figure 5, consists of a broad Gaussian velocity anomaly that is 86$\%$ slower than the background velocity of 3000m/s. Superposed on the Gaussian anomaly are vertical and horizontal gradients of 0.1 and -0.05 s^-1, respectively.

 

Circle.ps
Figure 5 Point source wavefield extrapolation example. Left: Velocity model with Gaussian-shaped anomaly 86$\%$ slower than the background velocity of 3000m/s. Superposed over top are vertical and horizontal gradients of 0.1 and -0.05km/s per km, respectively, and the 5 Hz ray-coordinate system. Middle: The 5Hz monochromatic wavefield. Right: Broadband wavefield calculated using a 0.2-25Hz frequency band.

The first test involved using a point source located at 3000m. Rays were computed between $-60^{\circ}$ and $60^{\circ}$ assuming an initial radius of 200m. Phase-ray wavefield extrapolation was then carried out with a constant $\Delta \t$ spacing of 0.0005s at a 5Hz frequency. The resulting ray-coordinate system, superposed on the left panel of Figure 5, is smooth and triplication-free. The middle panel presents the corresponding 5Hz monochromatic wavefield interpolated from the ray-coordinate system to a Cartesian mesh of spacing $\Delta x=\Delta z=10$m. These two panels illustrate that both the rayfield and wavefield successfully overturn. Wavefield wavelengths are observed to compress in the region of slow velocity about the Gaussian anomaly, and to expand at greater depths. The right panel presents the broadband image constructed for frequencies between 2-35Hz. All wavefield frequencies were extrapolated on a stationary 5Hz ray coordinate system.

The second example, shown in Figure 6, is the plane-wave equivalent to Figure 5. The panels in Figure 6 are similar to those presented in the previous figure.

 

Circle.pw
Figure 6 Extrapolation example for plane-wave with -10 dip. Left: Velocity model consisting of a Gaussian-shaped anomaly 86$\%$ slower than the background velocity of 3000m/s. Superposed are vertical and horizontal gradients of 0.1 and -0.05km/s per km, and the calculated 5Hz ray-coordinate system. Middle: The 5Hz monochromatic wavefield. Right: Broadband image calculated using a 0.2-25Hz frequency band.

The initial coordinate system and wavefield tilt angle was -10, and the spacing between individual rays was set at 20m. The left and middle panels show the 5Hz rayfield and the corresponding 5Hz wavefield, respectively. Again, the rayfield is observed to compress along coordinate $\gamma$ as it nears the center of the Gaussian anomaly leading to increased amplitudes and shorter wavelengths. The right panel presents the broadband wavefield calculated in the 0.2-25Hz frequency band. Again, all wavefield frequencies were extrapolated on a stationary 5Hz ray-coordinate system. As in the previous figure, the broadband result overturns and is triplication-free.

The next example demonstrates adaptive phase-ray wavefield extrapolation in a Gulf of Mexico salt model. The background velocity of the model, shown in the left panel of Figure 7, is a typical Gulf of Mexico v(z) velocity gradient.

 

Salt.ps
Figure 7 Point source extrapolated in a typical Gulf of Mexico velocity model. Left: Salt velocity model consisting of a typical Gulf of Mexico v(z) velocity gradient, with a salt body of 4700m/s wavespeed superposed at depth, and the calculated 5Hz monochromatic rayfield. Middle: The 5Hz monochromatic wavefield derived. Right: Broadband image computed for the 2-35Hz frequency band.

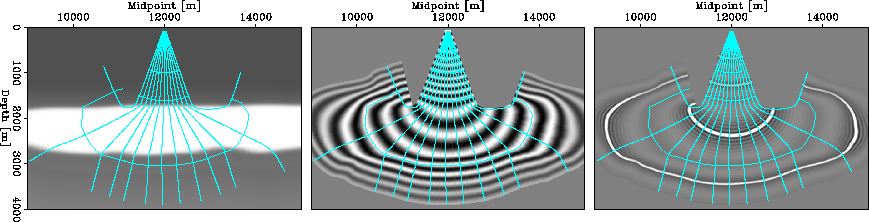The superposed salt body is characterized by a higher wavespeed (4700m/s) and a somewhat rugose bottom of salt interface. A point source was modeled at surface position 12000m with a starting radius of 200m. The initial angular coverage was bounded by $\gamma_{min}=-22^{\circ}$ and $\gamma_{max}=20^{\circ}$ because shooting beyond this angular range lead to ray-coordinate triplication. The superposed rayfield in the left panel demonstrates the effect of strong velocity contrasts and a rugose interface between the bottom of salt body and the enveloping sediments. At angles tending away from vertical (i.e. $\theta$=0), rays increasingly refract in accordance with Snell's law, become horizontal, impinge on the salt-sediment interface, and eventually refract upward at fairly steep angles. The middle and right panels present the 5Hz monochromatic and 2-35Hz broadband wavefields, respectively. Again, the ray-coordinate system in the right panel was assumed to be stationary, and all frequencies were extrapolation on 5Hz rayfield.