Complex earth experiments

Despite the success in removing alias artifacts with the above two methodologies, use of the bandlimited source function or the bandlimited imaging condition in areas of complex geology has one substantial limitation. Both strategies bandpass the wavefields at some point during the migration which effectively introduces focusing of the source illumination beam that propagates through the model. 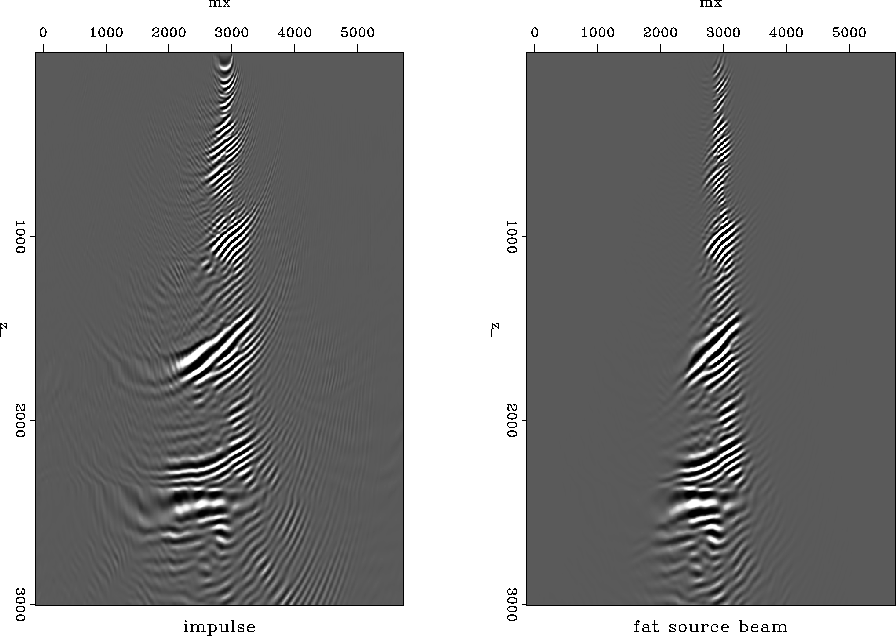This is due to elimination of k_x energy in the process. Figure 5 illustrates this effect using a shot modeled over the Marmousi data set. The left panel shows an image generated from the single shot with no restrictions imposed during migration. The right panel however used the spatially bandpassed source function. The introduction of low spatial frequencies into the initial condition of the source wavefield effectively changes the impulse into a short planewave. While this is appropriate to limit aliasing when all the shots are summed, the focusing of the beam directly down is inappropriate. To limit the dip-spectrum of the geology appropriate to our sampling thereof, we have limited the directionality of the source wavefield to near vertical as well.

 

marm
Figure 5 Left: Image from a single shot of the Marmousi data conventionally migrated and with anti-aliasing limits. The limited propagation angles are inappropriate. Center: Full bandwidth shot image. Right: Dip-limited image via partial convolution imaging condition.

Instead, our last methodology attempts to include all propagation directions by choosing portions of the wavenumber spectrum of the receiver wavefield that are appropriately limited for each component of the source wavefield (or vice-versa). While the goal of the imaging condition is a cross-correlation of the two wavefields followed by extraction of the zero time-lag as shown in equation (4), the process in effect multiplies across the space axis. Further, to calculate offset, a spatial cross-correlation without summation is employed. The Fourier dual of these two implicit operations are convolution and multiplication respectively. Thus, by transforming our wavefields into the wavenumber domain, the imaging condition takes the form of the convolution
$$\begin{multline} I(x;h)\vert _z,\omega= R(x-h) S^*(x+h)I(k_x;h) \vert _z,\omega=... ...lde{R}(k_x=k_r-j,z,\omega) \tilde{S}^*(k_s=j,z,\omega) e^{-ijh}. \end{multline}$$
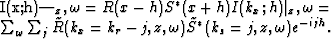
Inspecting the above, we notice that the counting subscript j is actually the wavenumber offset axis with with the exponential inverse Fourier transforming the axis during summation to give a single offset panel. Thus, by not summing this dimension, we build the Fourier transform of the offset axis.

Using this formulation, and the fact that k_r - k_s = k_h, we can bandlimit the image space by only allowing offset wavenumber combinations where k_r - k_s is less than the prescribed bandlimit. Thus, while calculating k_x wavenumbers for the image space, only a limited and varying band from the offset axis is considered. In this manner, we can limit reflectors to different offset spectra depending on their structural dip. 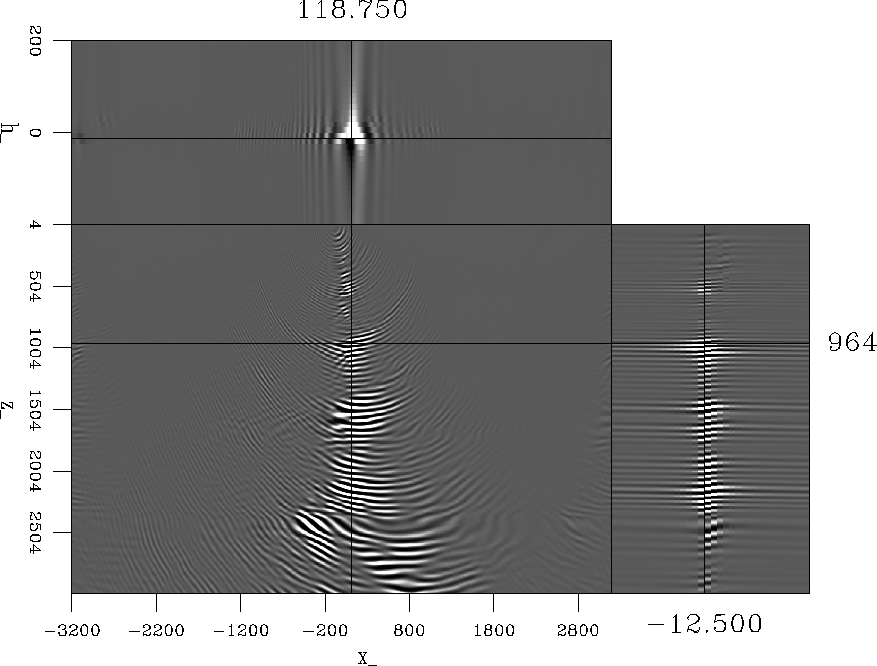Figure (6) shows the result of this implementation. Several features are prominent. First, the thick, fast layer at (3000m, 2500m) contains dipping energy that is not in the impulse response. This is a dip ringing due to implementing a hard cutoff in the Fourier domain when selecting wavenumbers for imaging. This noise should cancel during summation of many shots.

 

off-cube
Figure 6 Single shot image from the band-limited convolutional imaging condition. The wave-number bandwidth was limited to 1/8 of the receiver Nyquist limit.

Unfortunately, the convolutional imaging condition has Fourier domain periodicity problems that are well avoided by operating in the space domain. Further, there did not seem to be significant improvement over illumination angle as compared to the two previous methods proposed. Finally, given that our effective range of sub-surface offset is actually quite limited, the huge cost differential, O(n_x n_h) vs. O(n_x²), makes the decision for us.