




Next: Limitations
Up: THEORY
Previous: THEORY
I found that squaring the semblance values 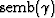 produced a better
result than the semblance values themselves. My resulting
cdf
produced a better
result than the semblance values themselves. My resulting
cdf 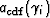 function was then
function was then
| 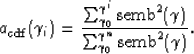 |
(11) |
In addition, I need to account for the fact that I am not scanning over
all possible 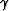 values. I introduced a constant parameter gmax
that scaled my
values. I introduced a constant parameter gmax
that scaled my  values so that that one standard deviation of
values so that that one standard deviation of  might correspond to 2-5 standard deviations
might correspond to 2-5 standard deviations  .
.
Finally, we are going to a precondition the model Fomel et al. (1997) with
the inverse of 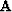 and solve the problems
in terms of the variable
and solve the problems
in terms of the variable 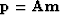 ,
,
| 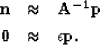 |
|
| (12) |





Next: Limitations
Up: THEORY
Previous: THEORY
Stanford Exploration Project
5/23/2004
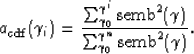
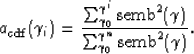
![]() and solve the problems
in terms of the variable
and solve the problems
in terms of the variable ![]() ,
,