




Next: THEORY
Up: R. Clapp: Velocity uncertainty
Previous: MULTIPLE REALIZATIONS REVIEW
Tomography for migration velocity analysis is
a non-linear problem that we linearize
around an initial slowness model. In this discussion, I will
be talking about the specific case of ray based tomography but
most of the discussion is valid for other tomographic operators.
We can linearize the problem around an initial slowness model and
obtain a linear relation 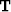 between
the change in travel times
between
the change in travel times 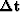 and
change in slowness
and
change in slowness 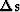 :
:
| 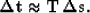 |
(6) |
Certain components of the velocity model are better determined than others.
As a result we need to either choose an intelligent model parameterization Cox et al. (2003)
or regularize the model. I prefer the regularizing approach so that I can easily
incorporate a priori information.
I impose a regularization operator that tends to smooth
the velocity according to reflector dip Clapp (2001b).
My resulting fitting goals then become
| 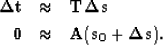 |
|
| (7) |
where 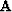 is a steering filter. In this paper I will do
downward
continuation based migration Ristow and Ruhl (1994); Stoffa et al. (1990)
and then
constructing angle gathers Prucha et al. (1999); Sava and Fomel (2000).
Biondi and Symes (2003)
and Biondi and Tisserant (2004) showed
that the travel time error is related to the
reflector dip
is a steering filter. In this paper I will do
downward
continuation based migration Ristow and Ruhl (1994); Stoffa et al. (1990)
and then
constructing angle gathers Prucha et al. (1999); Sava and Fomel (2000).
Biondi and Symes (2003)
and Biondi and Tisserant (2004) showed
that the travel time error is related to the
reflector dip  , local slowness
, local slowness 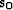 , depth z0, and
the velocity model scaled by
, depth z0, and
the velocity model scaled by 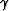 through
through
| 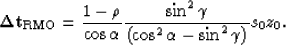 |
(8) |
One of the best ways to scan over 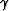 is by doing Stolt
Residual Migration (SRM) Sava (1999a,b). In
Clapp (2002b) I showed how we can
obtain better ray-based tomography results by doing SRM scanning
versus simple vertical move-out analysis.
is by doing Stolt
Residual Migration (SRM) Sava (1999a,b). In
Clapp (2002b) I showed how we can
obtain better ray-based tomography results by doing SRM scanning
versus simple vertical move-out analysis.





Next: THEORY
Up: R. Clapp: Velocity uncertainty
Previous: MULTIPLE REALIZATIONS REVIEW
Stanford Exploration Project
5/23/2004