 |
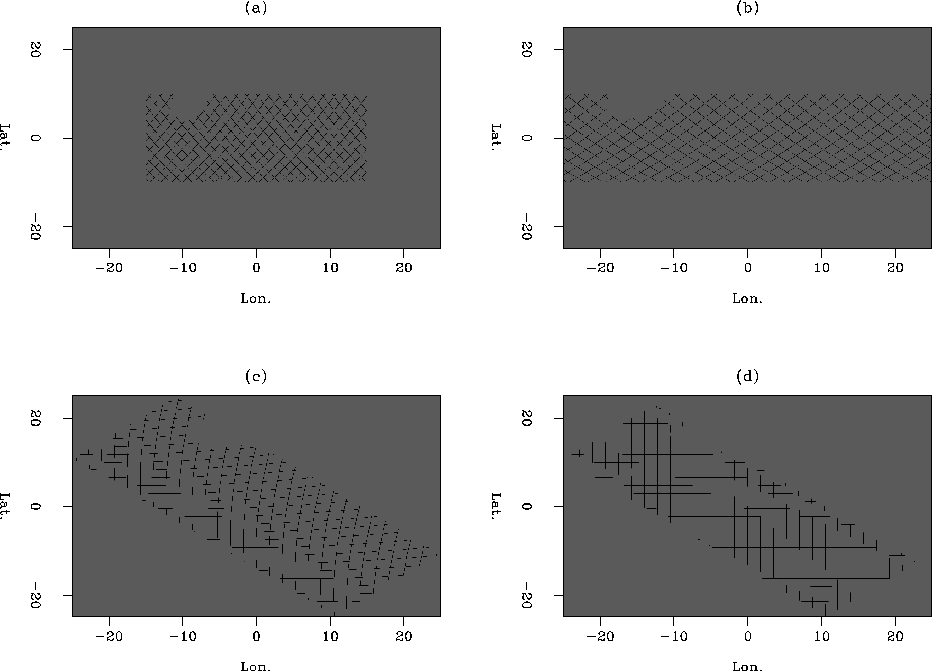
Figure 3 The steps used in warping the coordinate system.(a): Original model; (b): Stretching and centering; (c): Rotation; (d): Parabolic shifts.
The existing data are collected in a series of ascending and descending crossing tracks. The goal is to transform the model space so that it more closely resembles the pattern in which the data was collected, which is in two sets of crossing tracks. This can be done by first stretching the longitudinal axis so that the tracks are orthogonal, subtracting the mean values of the coordinates of the data, rotating the data so that the tracks are aligned North-South and East-West, applying two parabolic shifts along a rotated axis, and then finally breaking the data up into ascending and descending tracks and griding the data. This process is shown in Figure 3.
 |
The method used to warp the model space is not especially important. It would perhaps be better to use specific coordinates of the data space, but this warping accomplishes the same end goal of having straightened orthogonal tracks. We can use the same warped grid for our model space, allowing us to use a similar methodology that we used for the regularly-sampled data problem. The two sets of orthogonal tracks with missing data is very similar to a problem shown by Claerbout 1999, where a pair of 1D PEFs are used to fill in missing data. This can be expressed as
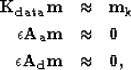 |
||
| (4) |
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
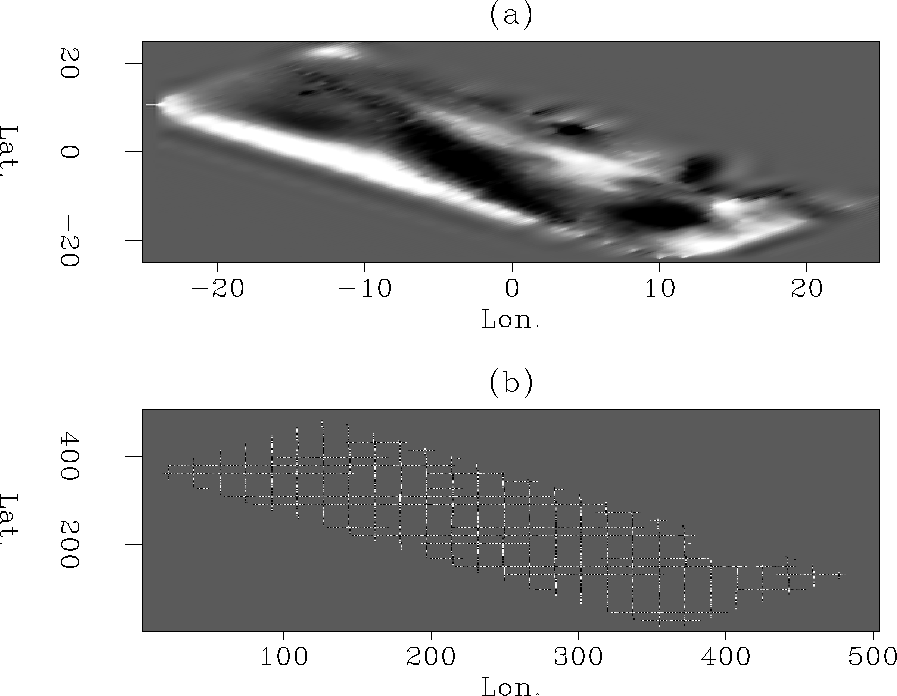
The results of this approach are good. The general trend of the data is interpolated, and the spreading ridge is clearly present in the model, which is not the case with Laplacian interpolation. Since this method only deals with the merged tracks, another method which uses the two track sets separately is tested next.
In this second method, the following fitting goals are solved:
| |
||
| (5) |
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
The residual space is now twice the size as that for the fitting goals in equation (4), since the ascending and descending tracks are now dealt with separately. This approach appears to also be successful, although some effects of the PEF are present in the data, making the result look like a roughened result. The spreading ridge can be easily delineated. The residual space is interesting to look at, as the influence of the two sets of tracks can be seen in the different portions of the residual. The imprint of the data has disappeared from one half of the residual and has appeared in the other.