




Next: Tomography
Up: Guitton et al.: Velocity
Previous: Introduction
Estimating time shifts is a two step procedure where local stepouts are first
estimated and then integrated. The goal of dip estimation is to find
a local stepout, ph, that destroys the
local plane wave such that,
| 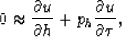 |
(1) |
where u is the wavefield at time  , midpoint x and offset h.
For all gathers, we evaluate the slope ph with
a method based on high-order
plane-wave destructor filters Fomel (2002). This technique
has the advantage of being accurate for steep dips. The estimation
of ph is based on a non-linear algorithm (Gauss-Newton method) that
includes a regularization term. This regularization smooths dips
across offset and CMP location.
One problem with the current technique is that the dip
estimation algorithm cannot properly handle conflicting dips.
This can be troublesome when, for instance, multiples are present in the data.
To solve this problem, Fomel (2002) and
Brown (2002) show how two dips can be
estimated. Then if multiple reflections are present, the stepouts
corresponding to the primaries are kept and those of the multiples are
rejected.
, midpoint x and offset h.
For all gathers, we evaluate the slope ph with
a method based on high-order
plane-wave destructor filters Fomel (2002). This technique
has the advantage of being accurate for steep dips. The estimation
of ph is based on a non-linear algorithm (Gauss-Newton method) that
includes a regularization term. This regularization smooths dips
across offset and CMP location.
One problem with the current technique is that the dip
estimation algorithm cannot properly handle conflicting dips.
This can be troublesome when, for instance, multiples are present in the data.
To solve this problem, Fomel (2002) and
Brown (2002) show how two dips can be
estimated. Then if multiple reflections are present, the stepouts
corresponding to the primaries are kept and those of the multiples are
rejected.
Dips estimates lead to a vector of local stepouts 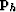 that are integrated one CMP at a time to obtain time shifts.
Dips are smoothed along both
spatial directions but not in time
that are integrated one CMP at a time to obtain time shifts.
Dips are smoothed along both
spatial directions but not in time  .
To enforce smoothness in the
.
To enforce smoothness in the  direction
Lomask and Guitton (2004) introduce a time
component
direction
Lomask and Guitton (2004) introduce a time
component 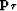 to
to 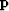 .
The relationship between the local time shift vector,
.
The relationship between the local time shift vector, 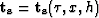 and the local dip vector
and the local dip vector 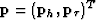 ((.)T being the transpose) at a constant x is:
((.)T being the transpose) at a constant x is:
| 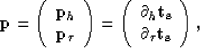 |
(2) |
where 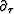 and
and 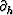 are the partial derivative in
are the partial derivative in
 , h respectively.
In practice, we choose
, h respectively.
In practice, we choose 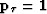 and control the amount of
smoothness by introducing a trade-off parameter
and control the amount of
smoothness by introducing a trade-off parameter  as follows Lomask and Guitton (2004):
as follows Lomask and Guitton (2004):
| 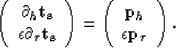 |
(3) |
Using equation (3) we wish to minimize
the length of a vector 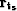 that measures the difference
between
that measures the difference
between 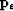 and
and 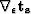 as follows:
as follows:
| 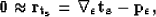 |
(4) |
where 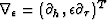 ,
and
,
and 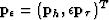 .We then minimize the following objective function:
.We then minimize the following objective function:
| 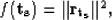 |
(5) |
where 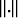 is the L2 norm.
By increasing
is the L2 norm.
By increasing  , the estimated time shifts
, the estimated time shifts 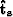 become smoother in time.
We solve equation (5) analytically in the Fourier domain
Lomask (2003), which speeds up the estimation of
become smoother in time.
We solve equation (5) analytically in the Fourier domain
Lomask (2003), which speeds up the estimation of 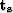 :
:
| ![\begin{displaymath}
{\bf \hat t_s} \quad = \quad {\rm FFT_{\rm 2D}}^{-1} \left[{...
...epsilon Z_\tau^{-1} +2+2\epsilon -Z_h -\epsilon Z_\tau} \right]\end{displaymath}](img25.gif) |
(6) |
where
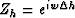 and
and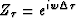 .The dip integration yields the desired time shifts
plus a constant, i.e., a DC frequency component.
The zero frequency component is removed by subtracting the near offset
panel from the other offsets. Therefore, the time shifts are a
measure of the moveout errors relative to the near-offset panel.
At the end of the dip integration process, we end up with a map of
time shifts,
.The dip integration yields the desired time shifts
plus a constant, i.e., a DC frequency component.
The zero frequency component is removed by subtracting the near offset
panel from the other offsets. Therefore, the time shifts are a
measure of the moveout errors relative to the near-offset panel.
At the end of the dip integration process, we end up with a map of
time shifts, 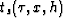 . These time shifts can be used to
flatten the CMP gathers without any velocity analysis.
Our goal, however, is to find an interval velocity
function consistent with the estimated time shifts using
a tomographic inversion procedure.
. These time shifts can be used to
flatten the CMP gathers without any velocity analysis.
Our goal, however, is to find an interval velocity
function consistent with the estimated time shifts using
a tomographic inversion procedure.





Next: Tomography
Up: Guitton et al.: Velocity
Previous: Introduction
Stanford Exploration Project
5/23/2004
![]() that are integrated one CMP at a time to obtain time shifts.
Dips are smoothed along both
spatial directions but not in time
that are integrated one CMP at a time to obtain time shifts.
Dips are smoothed along both
spatial directions but not in time ![]() .
To enforce smoothness in the
.
To enforce smoothness in the ![]() direction
Lomask and Guitton (2004) introduce a time
component
direction
Lomask and Guitton (2004) introduce a time
component ![]() to
to ![]() .
The relationship between the local time shift vector,
.
The relationship between the local time shift vector, ![]() and the local dip vector
and the local dip vector ![]() ((.)T being the transpose) at a constant x is:
((.)T being the transpose) at a constant x is: