|
multi_correct_v_2
Figure 1 The velocity function is V(z)=1.5+.5z km/s. The target has a fixed position, azimuth ( | 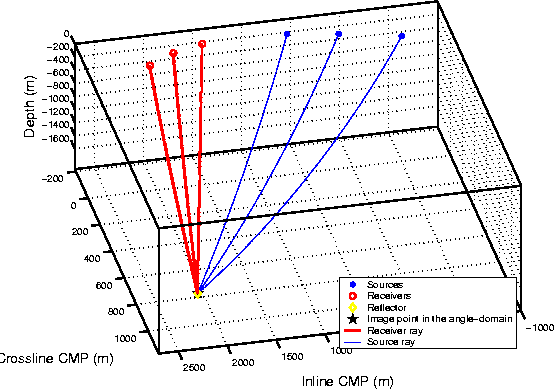 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
By assuming the velocity is constant around the image point,
all the elements (rays, normal, image points)
are contained in one plane: the plane of the propagation.
By an appropriate change of
coordinates, this 3-D problem with correct migration velocity
can be locally transformed in
a 2-D problem, and the 2-D theory analyzed by
Biondi and Symes (2003) be applied.
The offset-to-angle transformation must be adapted though.
).
By assuming the velocity is constant around the image point,
all the elements (rays, normal, image points)
are contained in one plane: the plane of the propagation.
By an appropriate change of
coordinates, this 3-D problem with correct migration velocity
can be locally transformed in
a 2-D problem, and the 2-D theory analyzed by
Biondi and Symes (2003) be applied.
The offset-to-angle transformation must be adapted though.
|
multi_correct_v_2
Figure 1 The velocity function is V(z)=1.5+.5z km/s. The target has a fixed position, azimuth ( |  |