|
spmig
Figure 14 Shot-profile migration sketch. Sources (a) and receivers (b) are extrapolated in the same ray coordinate system which is appropriate for overturning waves. | 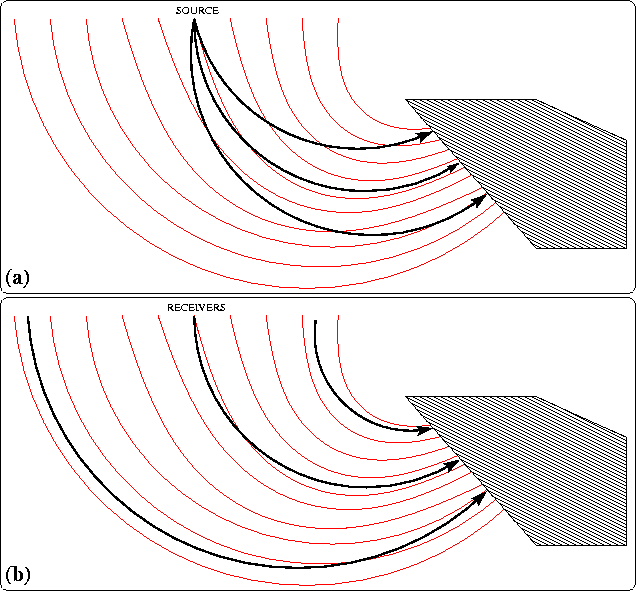 |
|
spmig
Figure 14 Shot-profile migration sketch. Sources (a) and receivers (b) are extrapolated in the same ray coordinate system which is appropriate for overturning waves. |  |