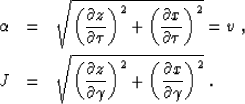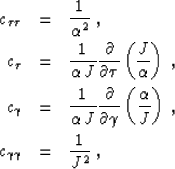2-D point-source ray coordinates

For the case of 2-D point-source ray coordinates the acoustic wave equation (6) takes the form  

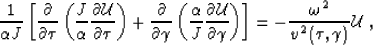$$\frac{1}{\AA J} \left[\frac{\partial } {\partial \t } \left(... ... = - \frac{\omega^2}{v^2\left(\t ,\gamma\right)} \mathcal{U}\;,$$ (31)

where, by definition,

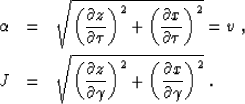$$\begin{eqnarray} \AA & = & \sqrt{ \left(\frac{\partial z}{\partial \t } \right)... ...t)^2 + \left(\frac{\partial x}{\partial \gamma } \right)^2 } \;.\end{eqnarray}$$ (32)

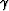The extrapolation axis is $\t$ (one-way traveltime from the source) and $\gamma$ is the shooting angle at the source.

We can expand the parentheses in equation (31)

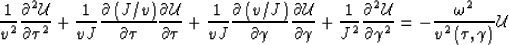$$\frac{1}{v^2} \frac{\partial^2 \mathcal{U}}{\partial \t^2} ... ...} = - \frac{\omega^2}{v^2\left(\t ,\gamma\right)} \mathcal{U}\;$$ (33)

and make the notations

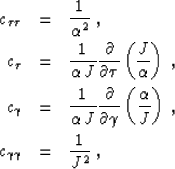$$\begin{eqnarray} \c_{\t\t}&=& \frac{1}{\AA^2} \;,\nonumber \\ \c_{\t }&=& \frac{... ...{J}\right) \;,\nonumber \\ \c_{\gamma\gamma}&=& \frac{1}{ J^2} \;,\end{eqnarray}$$ (34)

from which the acoustic wave equation for 2-D point-source ray coordinates becomes:

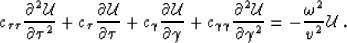$$\c_{\t\t}\frac{\partial^2 \mathcal{U}}{\partial \t^2} + \c_{... ...{U}}{\partial \gamma^2} = - \frac{\omega^2}{v^2} \mathcal{U}\;.$$ (35)

The 2-D dispersion relation is

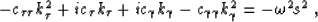$$- \c_{\t\t}k_\t^2 +i\c_{\t }k_\t +i\c_{\gamma}k_\gamma - \c_{\gamma\gamma}k_\gamma^2 = - \omega^2\ss^2 \;,$$ (36)

from which we can obtain the one-way wave equation for 2-D point-source ray coordinates:

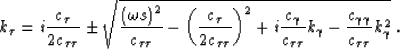$$k_\t= i \frac{\c_{\t }}{2\c_{\t\t}} \pm \sqrt{ \frac{\left(\... ...}}k_\gamma - \frac{\c_{\gamma\gamma}}{\c_{\t\t}}k_\gamma^2 }\;.$$ (37)

C