




Next: 2-D point-source ray coordinates
Up: Sava and Fomel: Riemannian
Previous: REFERENCES
Neglecting wave propagation in the directions orthogonal to 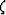 , one can
reduce the wave equation (6) to the form of the ordinary
differential equation
, one can
reduce the wave equation (6) to the form of the ordinary
differential equation
| 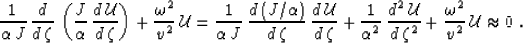 |
(25) |
The high-frequency (WKBJ) asymptotics for the solution of
equation (25) can be obtained by using a trial solution
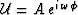 , substituting it in equation (25) and evaluating
terms with the same order of
, substituting it in equation (25) and evaluating
terms with the same order of 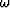 . The highest asymptotic order yields an
equation for the phase function
. The highest asymptotic order yields an
equation for the phase function 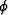 :
:
| 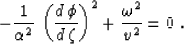 |
(26) |
The next asymptotic order produces an equation for the amplitude function A:
| 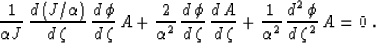 |
(27) |
Rearranging equation (26) to the form
| 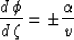 |
(28) |
and equation (27) to the form
| ![\begin{displaymath}
\frac{d\,(\log{A})}{d\,\zeta} =
- \frac{1}{2}\,\left[
\f...
...ta}
+ \frac{d\,\left(\log{(\AA/v)}\right)}{d\,\zeta}\right]\;,\end{displaymath}](img91.gif) |
(29) |
we can solve them explicitly to obtain the WKBJ approximation for the wave
traveling preferentially in the 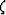 direction:
direction:
| ![\begin{displaymath}
\mathcal{U}_1 \approx \mathcal{U}_0\,\left(\frac{v_1\,J_0}{...
...
\int\limits_{\zeta_0}^{\zeta_1} \frac{\AA}{v}\,d\zeta
\right]}\end{displaymath}](img92.gif) |
(30) |
In the case of the ray coordinate system, equation (30) corresponds
to the Green's function approximation commonly employed in Kirchhoff imaging.
Accounting for the wave propagation in the directions different from 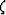 and constructing the solution numerically by finite differences allows us to
account for the finite-bandwidth wave propagation effects.
and constructing the solution numerically by finite differences allows us to
account for the finite-bandwidth wave propagation effects.
B





Next: 2-D point-source ray coordinates
Up: Sava and Fomel: Riemannian
Previous: REFERENCES
Stanford Exploration Project
10/14/2003
![]() , one can
reduce the wave equation (6) to the form of the ordinary
differential equation
, one can
reduce the wave equation (6) to the form of the ordinary
differential equation
![\begin{displaymath}
\mathcal{U}_1 \approx \mathcal{U}_0\,\left(\frac{v_1\,J_0}{...
...
\int\limits_{\zeta_0}^{\zeta_1} \frac{\AA}{v}\,d\zeta
\right]}\end{displaymath}](img92.gif)
![]() and constructing the solution numerically by finite differences allows us to
account for the finite-bandwidth wave propagation effects.
and constructing the solution numerically by finite differences allows us to
account for the finite-bandwidth wave propagation effects.