




Next: Born image perturbation
Up: WEMVA theory
Previous: WEMVA theory
The simplest linearization of equation (7)
is done by the Born approximation, which involves
an approximation of the exponential function
by a linear function 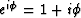 .
With this approximation, we obtain
.
With this approximation, we obtain
| 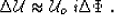 |
(9) |
We can, therefore, compute a linear wavefield perturbation
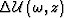 using a Born WEMVA operator:
using a Born WEMVA operator:
| ![\begin{displaymath}
\Delta \mathcal U= {\bf B}\left(\mathcal U_o\right)\left[\Delta s\right]\;,\end{displaymath}](img22.gif) |
(10) |
from which we can compute an image perturbation by summation
over frequency:
| 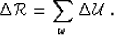 |
(11) |
For wave-equation MVA, we are interested in applying an
inverse WEMVA operator to a given image perturbation.
Therefore, the main challenge of the linearized WEMVA is
to estimate correctly 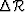 , i.e. an image perturbation
corresponding to the accumulated phase differences given by
all slowness anomalies above each image point.
, i.e. an image perturbation
corresponding to the accumulated phase differences given by
all slowness anomalies above each image point.
Given an image perturbation 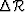 ,we can compute a wavefield perturbation
,we can compute a wavefield perturbation 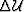 by the adjoint of the imaging operator,
from which we can compute a slowness perturbation
based on the background wavefield
by the adjoint of the imaging operator,
from which we can compute a slowness perturbation
based on the background wavefield 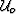 :
:
| ![\begin{displaymath}
\Delta s= {\bf B}^* \left(\mathcal U_o\right)\left[\Delta \mathcal U\right]\;.\end{displaymath}](img26.gif) |
(12) |





Next: Born image perturbation
Up: WEMVA theory
Previous: WEMVA theory
Stanford Exploration Project
10/14/2003
![]() using a Born WEMVA operator:
using a Born WEMVA operator:
![]() , i.e. an image perturbation
corresponding to the accumulated phase differences given by
all slowness anomalies above each image point.
, i.e. an image perturbation
corresponding to the accumulated phase differences given by
all slowness anomalies above each image point.
![]() ,we can compute a wavefield perturbation
,we can compute a wavefield perturbation ![]() by the adjoint of the imaging operator,
from which we can compute a slowness perturbation
based on the background wavefield
by the adjoint of the imaging operator,
from which we can compute a slowness perturbation
based on the background wavefield ![]() :
: