 |
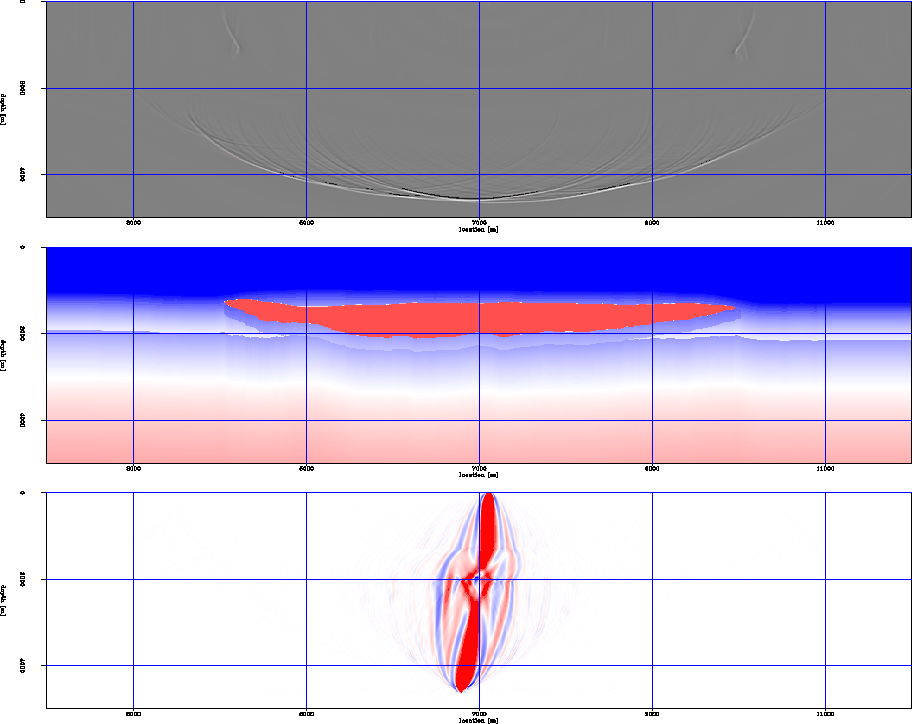
Figure 1 Fat rays in a salt velocity model. From top to bottom, the wavefield from a point source on the surface, the velocity model, and a fat ray from a point in the subsurface to the source.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
WEMVA is an optimization problem where the objective function is defined in the image space. As for other MVA methods, it tries to maximize the quality of the migrated image instead of trying to match the recorded data Sava and Symes (2002). In this respect, our method is related to Differential Semblance Optimization Symes and Carazzone (1991) and Multiple Migration Fitting Chavent and Jacewitz (1995). However, with respect to these two methods, our method has the advantage of exploiting the power of residual prestack migration to speed up the convergence, and it also gives us the ability to guide the inversion by geologic interpretation.
WEMVA benefits from the same advantages over traveltime estimation methods as wave-equation migration benefits over Kirchhoff migration. The most important among them are the accurate handling of complex wavefields which are characterized by multipathing, and the band-limited nature of the imaging process, which can handle sharp velocity variations much better than traveltime-based methods. Complex geology, therefore, is where WEMVA is expected to provide the largest benefits.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrate
the complications encountered under salt.
From top to bottom, we show the wavefield corresponding
to a point-source at the surface,
the background slowness model, and
a ``fat ray'' Woodward (1992)
from the source to a point in the subsurfaces.
Both examples show multipathing between source and receiver
which is naturally taken into account by WEMVA, but which
cannot be handled by simple traveltime tomography. Also, the
slowness model is not smooth as required by methods using ray
tracing.
illustrate
the complications encountered under salt.
From top to bottom, we show the wavefield corresponding
to a point-source at the surface,
the background slowness model, and
a ``fat ray'' Woodward (1992)
from the source to a point in the subsurfaces.
Both examples show multipathing between source and receiver
which is naturally taken into account by WEMVA, but which
cannot be handled by simple traveltime tomography. Also, the
slowness model is not smooth as required by methods using ray
tracing.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
WEMVA is based on a linearization of the downward-continuation operator using the Born approximation. This approximation leads to severe limitations on the magnitude and size of the anomalies that can be handled. Therefore, it cannot operate successfully in the regions of highest complexity. Other methods of linearization are possible Sava and Fomel (2002), but none allow for arbitrarily large anomalies.
In our early tests Biondi and Sava (1999),
we construct the image perturbation
using Prestack Stolt Residual Migration (PSRM)
Sava (2003). In summary, this residual
migration method provides updated images for new velocity maps
that correspond to a fixed ratio (![]() ) of the new velocity
with respect to the original velocity map. Residual migration
is run for various ratio parameters, and finally we pick the
best image by selecting the flattest gathers at every point.
) of the new velocity
with respect to the original velocity map. Residual migration
is run for various ratio parameters, and finally we pick the
best image by selecting the flattest gathers at every point.
The main disadvantage of building the image perturbation
using PSRM is that, for large velocity ratio parameters (![]() ),
the background and improved images can get more than
),
the background and improved images can get more than ![]() out of phase.
Therefore, the image perturbation computed by the Born forward
operator and the one computed by residual migration are fundamentally
different, and can have contradictory behaviors when using the
linearized WEMVA operator for inversion.
out of phase.
Therefore, the image perturbation computed by the Born forward
operator and the one computed by residual migration are fundamentally
different, and can have contradictory behaviors when using the
linearized WEMVA operator for inversion.
Alternative methods can be used to create image perturbations for WEMVA, directly in compliance with the Born approximation Sava and Biondi (2003). Those methods are not limited by the same restrictions as the Born methods, although their accuracy decreases with increasing deviation from the reference images. We refer to image perturbations created with this method as differential image perturbations.
In this paper we investigate various methods that can be used to compute image perturbations. Our goal is two fold: firstly, we show that we can do Rytov WEMVA basically using the same backprojection operator as the one involved in the Born approximation, but with a different definition of the image perturbation; secondly, we further investigate the differential approach to computing image perturbations and show that this method is similar to a phase-unwrapped Rytov, although it does not require any explicit phase unwrapping. Thus, the differential method is more practical and robust than a Rytov method, although it is less accurate and may require more non-linear iterations for convergence.
We begin with a review of wave-equation MVA with emphasis on the methods used to compute image perturbations. We then describe the Rytov approach to WEMVA and explore the relationship between the three different methodologies. Finally, we present a couple of synthetic examples for each of the image perturbation methods mentioned earlier and discuss the relationships between them.