Measuring dispersion

A simple and efficient way to measure the dispersion of plane waves in a shot gather has been described by McMechan and Yedlin . The method transforms a shot gather from the original (t,x) coordinate system to a (velocity, frequency) coordinate system, on which velocity can be picked as a function of frequency for each dispersion mode present in the data. The events to be analyzed this way must be linear. Surface waves fulfil this condition. 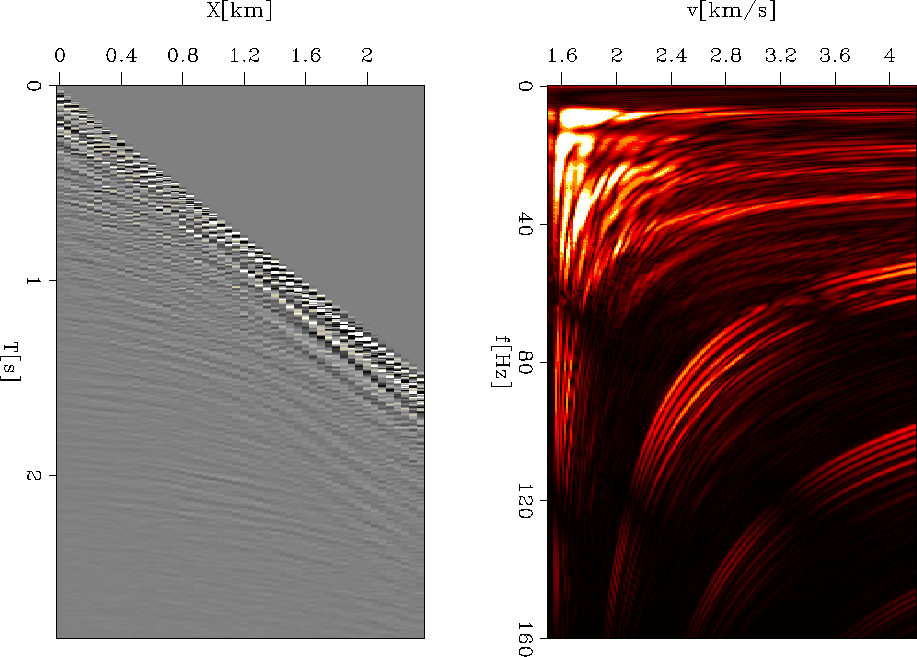An example of applying this method to a shot gather with ground roll stronger than the reflections is presented in Figure . The method consists of two steps: first the shot gather is slant-stacked, then it is Fourier-transformed along the time axis to obtain the power spectrum.

To investigate whether reflected events are dispersive, I transform hyperbolas (from a CMP gather this time, not from a shot gather) into straight lines using a T² - X² stretch. Linear event slopes will correspond to RMS velocities. I then apply the previously described algorithm for transforming the gather into an easy-to-pick (velocity, frequency) panel.

In practice, however, transforming to T² - X² coordinates then slant stacking is equivalent to summing along hyperbolic paths - a bare-bones Radon transform with no amplitude corrections. This cuts the cost in half and is the way I implemented it. Similar hyperbolic Radon transforms were used in velocity analysis, but they have been replaced in common practice by semblance panels. To obtain a semblance panel, instead of summing along hyperbolas, a statistical measure of coherence is computed along them. Feeding such a semblance panel into the dispersion analysis flow did not show improvement. The mathematics of the McMechan and Yedlin (1980) method seem to be geared towards actual summations along velocity-dependent paths. Deconvolution (which usually improves velocity analysis) did not result in visible changes either, which means that predictive deconvolution with the same filter for all traces in the dataset did not affect dispersion.

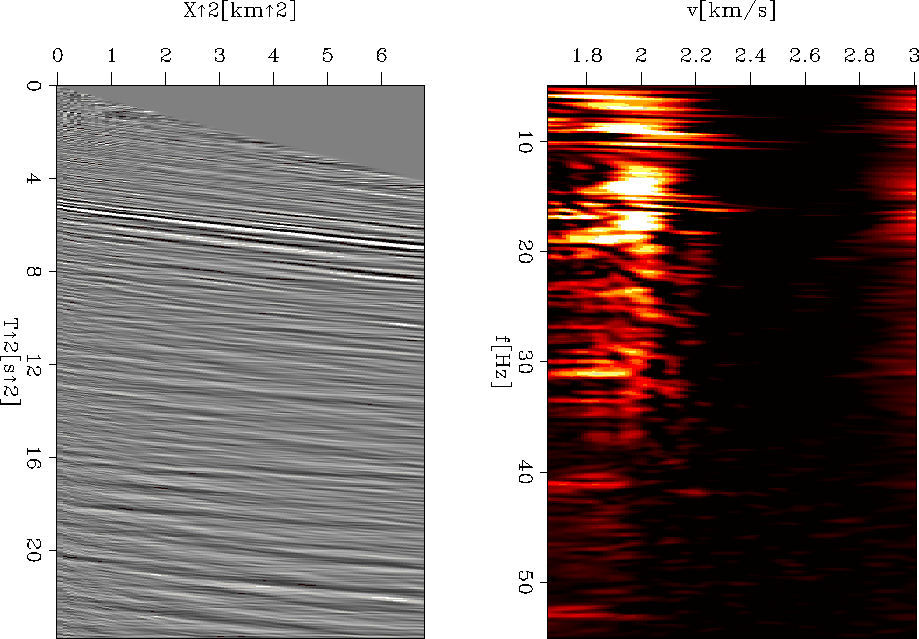
The results (bandpassed to eliminate DC components) are presented in Figure . Dispersion curves are much less visible than in the case of surface waves, but this may be because the number of reflections in the left panel of Figure is considerably greater than the number of distinct linear events in the left panel of Figure . This may lead to mutually destructive interference in the dispersion analysis panel. The inferable trend does not warrant a variation in velocity of more than 100m/s across the reflection seismic frequency spectrum. These conclusions from a single Mississippi Delta 2-D line cannot be generalized to all seismic reflection data. However, I did not find any literature or anecdotal evidence pointing to variations in body wave velocity of more than 100 m/s across the useful reflection seismic frequency range.

 

trytool
Figure 1 Example of applying the McMechan and Yedlin (1980) dispersion analysis method. Left: input shot gather. Right: output dispersion panel. Curved events represent various dispersion modes for surface waves. Other events correspond to different arrivals in the data (direct arrival, reflections, etc.).

 

petrix
Figure 2 Application of the McMechan and Yedlin (1980) dispersion analysis method to a CMP gather from which the surface waves have been eliminated by muting and f-k filtering. Left: virtual input. Right: output of the method. The frequency range is different from Figure because the data has been processed to highlight reflections and eliminate surface waves.