The approach that we take instead
is to first reduce these double-porosity laws (6)-(10) to an effective
single-porosity Biot
theory having complex frequency-dependent coefficients. The easiest
way to do this is to assume that phase 2 is entirely embedded in phase 1 so that
the average flux ![]() into and out of the averaging volume across the external
surface of phase 2 is zero. By
placing
into and out of the averaging volume across the external
surface of phase 2 is zero. By
placing ![]() into the compressibility laws (8),
the fluid pressure pf2 can be entirely eliminated from the theory.
In this case the double-porosity laws reduce to effective single-porosity
poroelasticity governed by laws of the form
(3) but with effective poroelastic
moduli given by
into the compressibility laws (8),
the fluid pressure pf2 can be entirely eliminated from the theory.
In this case the double-porosity laws reduce to effective single-porosity
poroelasticity governed by laws of the form
(3) but with effective poroelastic
moduli given by
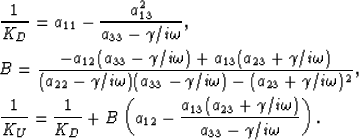 |
(11) | |
| (12) | ||
| (13) |
The complex frequency dependent ``drained'' modulus KD again defines the total volumetric response when the average fluid pressure throughout the entire composite is unchanged; however, the local fluid pressure in each phase may be non-uniform even though the average is zero resulting in mesoscopic flow and in KD being complex and frequency dependent. Similar interpretations hold for the undrained moduli KU and B. An undrained response is when no fluid can escape or enter through the external surface of an averaging volume; however, there can be considerable internal exchange of fluid between the two phases resulting in the complex frequency-dependent nature of both KU and B.