




Next: Double-Porosity Governing Equations
Up: REVIEW OF THE DOUBLE-POROSITY
Previous: REVIEW OF THE DOUBLE-POROSITY
Each porous phase is locally modeled as a porous continuum and
obeys the laws of poroelasticty [e.g., Biot (1962)]
| 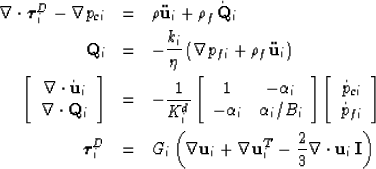 |
(1) |
| (2) |
| (3) |
| (4) |
where the index i represents the two phases (i=1,2).
The response fields in these equations
are themselves local volume averages taken over a scale
larger than the grain sizes but smaller than the mesoscopic
extent of either phase. The local fields are: 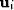 , the average displacement of the framework of grains;
, the average displacement of the framework of grains;
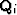 , the Darcy filtration
velocity; pfi, the fluid pressure; pci,
the confining pressure (total average
pressure); and
, the Darcy filtration
velocity; pfi, the fluid pressure; pci,
the confining pressure (total average
pressure); and
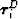 , the deviatoric (or shear) stress tensor.
In the linear theory of interest here, the overdots
on these fields denote a partial time derivative.
In the local Darcy law (2),
, the deviatoric (or shear) stress tensor.
In the linear theory of interest here, the overdots
on these fields denote a partial time derivative.
In the local Darcy law (2),  is the fluid viscosity and
the permeability ki is a linear time-convolution operator whose
Fourier transform
is the fluid viscosity and
the permeability ki is a linear time-convolution operator whose
Fourier transform 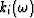 is called the ``dynamic permeability''
and can be modeled using the theory of Johnson et al. (1987)
(see the Appendix).
is called the ``dynamic permeability''
and can be modeled using the theory of Johnson et al. (1987)
(see the Appendix).
In the local compressibility law (3),
Kdi is the drained bulk modulus of phase i (confining pressure change divided
by sample dilatation under conditions where the fluid pressure does not change),
Bi is Skempton's (1954) coefficient of phase i
(fluid pressure change divided by confining pressure change for a sealed
sample), and 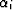 is the Biot and Willis (1957) coefficient of phase i defined as
is the Biot and Willis (1957) coefficient of phase i defined as
| 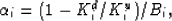 |
(5) |
where Kui is the
undrained bulk modulus (confining pressure
change divided by sample dilatation for a sealed sample).
In the present work, no restrictions to single-mineral isotropic grains
will be made.
Finally, in the deviatoric constitutive law (4),
Gi is the shear modulus of the framework of
grains. At the local level, all these poroelastic constants are taken to be
real constants. In the appendix we give the Gassmann (1951)
fluid-substitution relations that allow Bi and 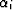 to be
expressed in terms of the porosity
to be
expressed in terms of the porosity 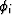 , the fluid and solid bulk
moduli Kf and Ks, and the drained modulus Kdi.
, the fluid and solid bulk
moduli Kf and Ks, and the drained modulus Kdi.





Next: Double-Porosity Governing Equations
Up: REVIEW OF THE DOUBLE-POROSITY
Previous: REVIEW OF THE DOUBLE-POROSITY
Stanford Exploration Project
10/14/2003
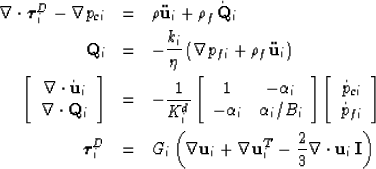
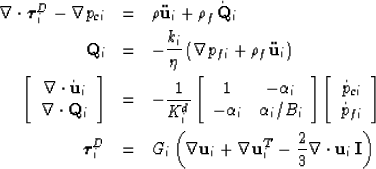
![]() is the Biot and Willis (1957) coefficient of phase i defined as
is the Biot and Willis (1957) coefficient of phase i defined as