




Next: REFERENCES
Up: Pride et al.: Seismic
Previous: CONCLUSIONS
In order to use the unified double-porosity framework of the present paper,
it is convenient to have models for the various porous-continuum constituent
properties.
For unconsolidated sands and soils, the frame moduli (drained bulk modulus Kd and
shear modulus G) are well modeled using the following variant of
the Walton (1987) theory [c.f., Pride (2003) for details]
| ![\begin{eqnarray}
K^d \!\!&=& \frac{1}{6} \left[\frac{4 (1-\phi_o)^2 n_o^2 P_o}{\...
...{\left\{1 + [16 P_e/(9 P_o)]^4\right\}^{1/24}},
\\ G &=& 3 K^d/5, \end{eqnarray}](img236.gif) |
(133) |
| (134) |
where Pe is the effective overburden pressure [e.g., 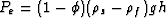 where
g is gravity and h is overburden thickness] and where Po is the effective
pressure at which all grain-to-grain contacts are established.
For Pe < Po, the coordination number n (average number of grain contacts
per grain) is increasing as (Pe/Po)1/2. For Pe > Po, the coordination
number remains constant n=no.
The parameter Po is commonly on the order of 10 MPa. As
where
g is gravity and h is overburden thickness] and where Po is the effective
pressure at which all grain-to-grain contacts are established.
For Pe < Po, the coordination number n (average number of grain contacts
per grain) is increasing as (Pe/Po)1/2. For Pe > Po, the coordination
number remains constant n=no.
The parameter Po is commonly on the order of 10 MPa. As 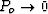 ,
the Walton (1987) result is obtained (all contacts in place starting from
Pe = 0). The porosity
of the grain pack is
,
the Walton (1987) result is obtained (all contacts in place starting from
Pe = 0). The porosity
of the grain pack is  and the compliance parameter Cs is defined
and the compliance parameter Cs is defined
| 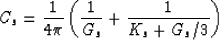 |
(135) |
where Ks and Gs are the mineral moduli of the grains.
For unimodal grain-size distributions and random grain packs, one typically has
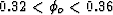 and 8 < no < 11.
and 8 < no < 11.
For consolidated sandstones, the frame moduli are modelled in the present paper
as [c.f., Pride (2003) for details]
| 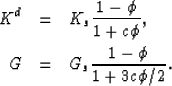 |
(136) |
| (137) |
The consolidation parameter c represents the degree of consolidation
between the grains and lies in the approximate range
2 < c < 20 for sandstones. If it is necessary to use a c greater
than say 20 or 30, then it is probably better to use the modified-Walton theory.
The undrained moduli Ku and B are conveniently and exactly
modeled using the Gassmann (1951) theory whenever the grains are
isotropic and composed of a single mineral. The results are
| 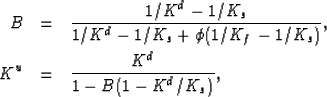 |
(138) |
| (139) |
from which the Biot-Willis constant  may be determined to be
may be determined to be
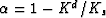 . These Gassmann results are often called
the ``fluid-substitution'' relations.
. These Gassmann results are often called
the ``fluid-substitution'' relations.
The dynamic permeability 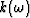 as modeled by Johnson et al. (1987)
is
as modeled by Johnson et al. (1987)
is
| ![\begin{displaymath}
\frac{k(\omega)}{k_o} = \left[\sqrt{1- i \frac{4}{n_J} \frac{\omega}{\omega_c} }
- i \frac{\omega}{\omega_c}\right]^{-1},
\end{displaymath}](img245.gif) |
(140) |
where the relaxation frequency 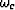 , which controls the frequency at which
viscous-boundary layers first develop, is given by
, which controls the frequency at which
viscous-boundary layers first develop, is given by
| 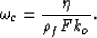 |
(141) |
Here, F is exactly the electrical formation factor when grain-surface
electrical conduction is not important and is conveniently
(though crudely) modeled using Archie's law 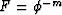 . The cementation
exponent m is related to the distribution of grain shapes (or pore topology)
in the sample and is
generally close to 3/2 in clean sands, close to 2 in shaly sands, and close to
1 in rocks having fracture porosity. The parameter nJ is, for convenience,
taken to be 8 (cylinder model of the porespace).
. The cementation
exponent m is related to the distribution of grain shapes (or pore topology)
in the sample and is
generally close to 3/2 in clean sands, close to 2 in shaly sands, and close to
1 in rocks having fracture porosity. The parameter nJ is, for convenience,
taken to be 8 (cylinder model of the porespace).





Next: REFERENCES
Up: Pride et al.: Seismic
Previous: CONCLUSIONS
Stanford Exploration Project
10/14/2003
![\begin{eqnarray}
K^d \!\!&=& \frac{1}{6} \left[\frac{4 (1-\phi_o)^2 n_o^2 P_o}{\...
...{\left\{1 + [16 P_e/(9 P_o)]^4\right\}^{1/24}},
\\ G &=& 3 K^d/5, \end{eqnarray}](img236.gif)
![\begin{eqnarray}
K^d \!\!&=& \frac{1}{6} \left[\frac{4 (1-\phi_o)^2 n_o^2 P_o}{\...
...{\left\{1 + [16 P_e/(9 P_o)]^4\right\}^{1/24}},
\\ G &=& 3 K^d/5, \end{eqnarray}](img236.gif)
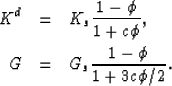
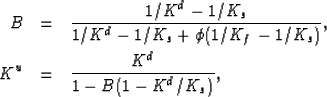
![]() as modeled by Johnson et al. (1987)
is
as modeled by Johnson et al. (1987)
is
![\begin{displaymath}
\frac{k(\omega)}{k_o} = \left[\sqrt{1- i \frac{4}{n_J} \frac{\omega}{\omega_c} }
- i \frac{\omega}{\omega_c}\right]^{-1},
\end{displaymath}](img245.gif)