Segmentation Methodology

The normalized segmentation method described by Shi and Malik (2000) is designed to look for clusters of pixels with similar intensity. To do this, it first creates a weight matrix relating each pixel to every other pixel within a local neighborhood. The strongest weights will be between pixels of similar intensity and close proximity to each other. The method then seeks to partition the image into two groups, A and B, by minimizing the normalized cut:

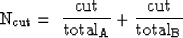$${\rm N_{cut} =\ {cut\over total_A } + {cut\over total_B} }$$ (1)

where cut is the sum of the weights cut by the partition. total_A is the total number of weights in Group A, and total_B is the total number of weights in Group B. Normalizing the cut by the total number of weights in each group prevents the partition from selecting overly-small groups of nodes.

The minimum of N_cut can be found by solving the generalized eigensystem:

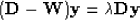$$({\bf D} - {\bf W})\bf y =\lambda {\bf D}\bf y$$ (2)

created from the weight matrix (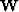${\bf W}$) and a diagonal matrix (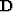${\bf D}$), with each value on the diagonal being the sum of each column of 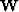${\bf W}$. The eigenvector (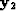${\bf y_2}$) with the second smallest eigenvalue is used to partition the image by taking all values greater than zero to be in one group, and its complement to be in the other.

 

• Application to seismic