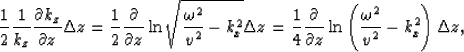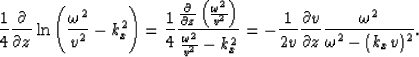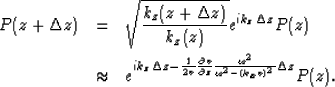Next: Conclusion
Up: Shan and Biondi: Residual
Previous: Amplitude preserving one-way wave
In this section, we demonstrate that the first order approximation of WKBJ is the same as the amplitude
preserving one-way wave equation for v=v(z).
The one-way wave equation with the WKBJ amplitude correction is
| 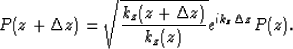 |
(7) |
The WKBJ amplitude correction term 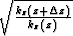 can be rewritten as
can be rewritten as
| 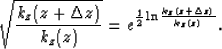 |
(8) |
Then 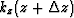 in equation (8) can be linearized to
in equation (8) can be linearized to 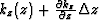 , so we have
, so we have
| 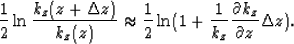 |
(9) |
From
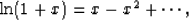
and
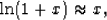
we have
| 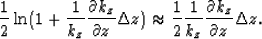 |
(10) |
Because
| 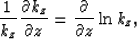 |
(11) |
and from the dispersion relation 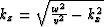 , we have
, we have
| 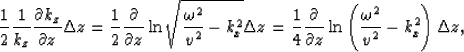 |
(12) |
and
| 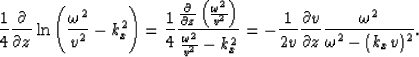 |
(13) |
From equation (8) to equation (13), we have
| 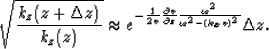 |
(14) |
So equation (7) can be rewritten as
| 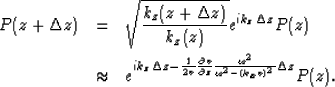 |
(15) |
| (16) |
Comparing the amplitude preserving one-way wave equation (equation (4))
with first order approximation of WKBJ (equation (16)),
we find they are same.
So we demonstrate theoretically that the amplitude preserving one-way wave equation is equivalent to the first
order approximation of WKBJ.





Next: Conclusion
Up: Shan and Biondi: Residual
Previous: Amplitude preserving one-way wave
Stanford Exploration Project
10/14/2003
![]()
![]()