| (1) |
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
Given an overcomplete dictionary for analysis, BP simply states the
goal of choosing the one representation of the signal whose
coefficients, ![]() , have the smallest l1 norm. The pursuit
then is searching through the dictionary for a minimum number of atoms
that will act as bases and represent the signal precisely. Mathematically,
this takes the form
, have the smallest l1 norm. The pursuit
then is searching through the dictionary for a minimum number of atoms
that will act as bases and represent the signal precisely. Mathematically,
this takes the form
| |
(2) |
Linear programming (LP) has a large literature and several techniques by which to solve problems of the form
| |
(3) |
Having recognized the format, one needs only choose among the available methods to solve an LP problem. BP chooses an interior point (IP) method as opposed to the simplex method of Claerbout and Muir (1973) to solve the LP. IP introduces a two loop structure to the solver: a barrier loop that calculates fabrication and direction variables, and an interior solver loop that uses a conjugate gradient minimization of the system derived from the current status of the solution and the derived directions. Heuristically, we begin with non-zero coefficients across the dictionary, and iteratively modify them, while maintaining the feasibility constraints, until energy begins to coalesce into the significant atoms of the sparse model space. Upon reaching this concentration, the method pushes small energy values to zero and completes the basis pursuit decomposition. For this reason, models where the answer has a sparse representation converge much more rapidly. If the model space is not sparse, or cannot be sparse, this is the wrong tool.
A particular benefit of adopting this structure to solve the decomposition problem lies in the primal-dual nature of interior point (as opposed to simplex) LP methods. For any minimization problem, the primal, there is a equally valid maximization problem, its dual, that can be simultaneously evaluated during the iterative solving process. It is known that at convergence, the primal and dual variables are the same. Thus, the separation between the primal and dual model space can be evaluated to provide a rigorous test for convergence. The two loop structure then takes the form of setting up a least squares problem that solves for the update to the dual variable, then evaluating the new solutions from this answer and testing the duality gap. When the difference is less than the tolerance proscribed by the user, the algorithm terminates.
The interior loop that uses a CG solver solves a system that looks like
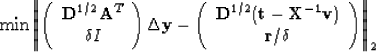 |
(4) |
During this brief explanation of the concept, only two user defined
parameters have been mentioned. The first is the desired tolerance
associated with the duality gap, and the second is ![]() . In a
realistic implementation there are, of course, a few more parameters.
They are largely functions of these two mentioned, automatically
updated in the IPLP algorithm, or constants.
. In a
realistic implementation there are, of course, a few more parameters.
They are largely functions of these two mentioned, automatically
updated in the IPLP algorithm, or constants.
![]() has interesting properties to discuss.
Saunders and Tomlin (1996) describes in detail the mathematics
associated with this approach. The regularization of the search
direction introduced with
has interesting properties to discuss.
Saunders and Tomlin (1996) describes in detail the mathematics
associated with this approach. The regularization of the search
direction introduced with ![]() actually makes this one of a class
of LP problems called perturbed, and introduces a minor change
to equation (3). Leaving those details to the reader, I
will address the choice of the parameter. Thankfully, the BP will
converge if
actually makes this one of a class
of LP problems called perturbed, and introduces a minor change
to equation (3). Leaving those details to the reader, I
will address the choice of the parameter. Thankfully, the BP will
converge if ![]() is anywhere between 1 and 4*10-4. If the
regularization parameter is small, the BP converges slowly, but to a
more precise solution that honors the data exactly.
As
is anywhere between 1 and 4*10-4. If the
regularization parameter is small, the BP converges slowly, but to a
more precise solution that honors the data exactly.
As ![]() , the central
equations solved in the inner loop become highly damped resulting in
three affects: 1) speedy convergence, 2) effective denoising, and 3)
less rigor attached to the ``subject to''
condition in equation (3). The
penalty is that the result lacks some sparsity and precision compared to
the result with a small value.
, the central
equations solved in the inner loop become highly damped resulting in
three affects: 1) speedy convergence, 2) effective denoising, and 3)
less rigor attached to the ``subject to''
condition in equation (3). The
penalty is that the result lacks some sparsity and precision compared to
the result with a small value.