Data size

The estimation problem we have set up requires a model space larger than we will typically use in migration. As mentioned above, traditional implementation of AMO Biondi et al. (1998) works like Kirchhoff migration. We define our model space (as sparse or as dense as we wish) and there sum in nearby traces with appropriate weights. The AMO procedure can be used as a fairly intelligent partial stack. By implementing the AMO as a regularization operator we are asking 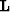$\bf L$ to map the trace from the irregular data space to the the regular space that our model exists on. If we have too coarse of a sampling in our model space we end up mapping numerous data points to each model point. If we think about data's behavior as a function of offset (fairly variable even after NMO) the danger of making too large of bins becomes apparent.

The problem is that our full model space is enormous. A small to mid-size dataset might have 1500 time samples, 1000 cmp_x, 1000 cmp_y, 128 h_x, and require 20 h_y. That amounts 15 TBs, exceeding the entire storage capacity of SEP. Even a small portion of the dataset (500 cmp_x, 200 cmp_y) will still consume 1.5 TB.