




Next: Regularization
Up: R. Clapp: AMO regularization:
Previous: R. Clapp: AMO regularization:
Most downward continuation methods require that the data lie on
a regular mesh.
To map the irregular recorded seismic data onto the regular mesh
is a far from trivial exercise.
A common approach in industry is to think of the problems in the same
way we approach Kirchhoff migration,
namely to loop over data space and spread into our regular
model space. The spreading operation is governed by something
like AMO Biondi et al. (1998), which maps data from one offset vector to
another.
If we think of the AMO operator 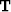 as mapping from the regular model space
as mapping from the regular model space 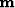 to the regular data space
to the regular data space 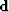 , our estimation procedure becomes,
, our estimation procedure becomes,
| 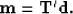 |
(1) |
This formulation suffers from all of the usual problems associated with
applying an adjoint operation. We are spraying into a regular mesh, but
the coverage is not regular. Areas with higher
concentration of data traces will tend to map to artificially higher amplitudes in the model
space.
We can do some division by hit count to help minimize this effect
but will still see some artifacts that come from approximating the
inverse with an adjoint.
We can think of turning (1) into an inversion
problem but, in addition to the high cost associated
with the AMO operationm we face the same stability issues that setting up
the migration problem as an inverse problem encounters. The null space of
the imaging operator tends to put high frequency noise in the model
space when cast as inverse problem.
Fomel (2001) suggested thinking of the problem more as a missing
data problem.
We can write the missing data problem in terms of the fitting goals
| 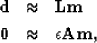 |
|
| (2) |
where 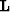 is a simple
interpolation operator (nearest-neighbor, linear, etc) and the real
work is done by the regularization operator
is a simple
interpolation operator (nearest-neighbor, linear, etc) and the real
work is done by the regularization operator 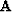 which describes
the relationship between the irregular data and the regular sampled model.
which describes
the relationship between the irregular data and the regular sampled model.
We can speed up the convergence of (2) by
preconditioning the model with 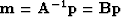 .
Our new fitting goals become,
.
Our new fitting goals become,
| 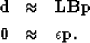 |
|
| (3) |
Biondi and Vlad (2001) suggested following the
approach of Claerbout and Nichols (1994) and Rickett (2001).
Instead of solving
the inverse problem, they suggest filtering the adjoint solution with a diagonal operator.
We obtain our filtering operator by first noting the least
squares inverse of the interpolation problem,
| 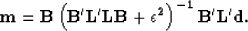 |
(4) |
We can think of equation (4) as filtering the adjoint solution
with the matrix 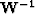 where,
where,
| 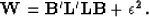 |
(5) |
The weighting matrix is (np x np) where np is the size of
our preconditioned model space.
This matrix will be generally diagonally dominant.
We can think of estimating a diagonal filtering operator 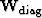 by using a reference model (in preconditioned model space)
by using a reference model (in preconditioned model space) 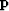 and applying
and applying
| ![\begin{displaymath}
\bf W_{{\rm diag}} = \frac{ {\rm\bf diag} \left[( \bf B' \bf...
...bf p_{ref} \right]}
{ {\rm \bf diag}\left(\bf p_{ref}\right)} .\end{displaymath}](img17.gif) |
(6) |
We can then get an estimate of our model through
| 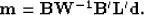 |
(7) |
![]() .
Our new fitting goals become,
.
Our new fitting goals become,