




Next: Evaluation of and
Up: REFERENCES
Previous: REFERENCES
Differentiating
equation (14)
and after some algebraic manipulation,
we obtain the following:
| 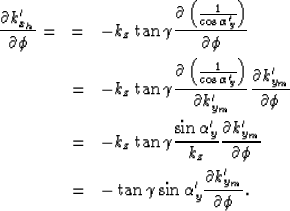 |
|
| |
| |
| (15) |
Differentiating
equation (13)
we can write the following:
| ![\begin{displaymath}
\frac{\partial k_{y_h}'}{\partial \phi}
=
k_z\tan\gamma
\le...
...{\partial \sin \alpha'_y}{\partial \phi}
\tan\alpha'_x
\right].\end{displaymath}](img51.gif) |
(16) |
To evaluate
equation (16)
we need 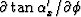 and
and
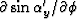 ;that is,
;that is,
| 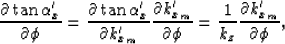 |
(17) |
and
| 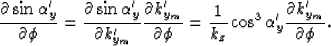 |
(18) |
Substituting
equation (17)
and
equation (18)
into
equation (16),
we finally obtain:





Next: Evaluation of and
Up: REFERENCES
Previous: REFERENCES
Stanford Exploration Project
10/14/2003
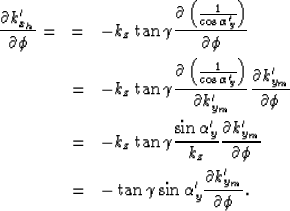
![\begin{eqnarray}
\frac{\partial k_{y_h}'}{\partial \phi}
&=&
k_z\tan\gamma
\left...
...'_y
\frac{\partial k_{y_m}'}{\partial \phi}
\right].
\nonumber
\\ \end{eqnarray}](img56.gif)