Imagine that the model residuals in equations (3) and (4) consisted of spikes separated by relatively large distances. Then the interval velocity ![]() would be piecewise smooth with jumps at the spike locations, which is what we desire. However in solving (2)-(4) we use the least-squares criterion - minimization of the
would be piecewise smooth with jumps at the spike locations, which is what we desire. However in solving (2)-(4) we use the least-squares criterion - minimization of the ![]() norm of the residual. Any spikes in the residual will be attenuated. To do this, the solver smooths the velocity across the spike location.
norm of the residual. Any spikes in the residual will be attenuated. To do this, the solver smooths the velocity across the spike location.
It is known that the ![]() norm is less sensitive to spikes in the residual Claerbout and Muir (1973); Darche (1989); Nichols (1994).
norm is less sensitive to spikes in the residual Claerbout and Muir (1973); Darche (1989); Nichols (1994). ![]() norm minimization makes the assumption that the residuals have an exponential distribution, a ``long-tailed'' distribution relative to the Gaussian. Here, we compute nonlinear model residual weights which force a Cauchy distribution, another long-tailed distribution which approximates an exponential distribution Youzwishen (2001).
norm minimization makes the assumption that the residuals have an exponential distribution, a ``long-tailed'' distribution relative to the Gaussian. Here, we compute nonlinear model residual weights which force a Cauchy distribution, another long-tailed distribution which approximates an exponential distribution Youzwishen (2001).
We perform the following non linear iterations:
starting with ![]() , at the kth iteration the algorithm solves
, at the kth iteration the algorithm solves
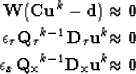 |
||
| (5) |
![\begin{eqnarray}
{\bf Q_{\tau}}^{k-1} = \frac{1}{\left[1+\left( \frac{{ \bf D_{\...
...ac{{ \bf D_x u}^{k-1}}{\alpha_x} \right)^2 \right]^{\frac{1}{2}}},\end{eqnarray}](img16.gif) |
(6) | |
| (7) |