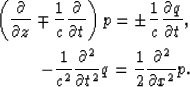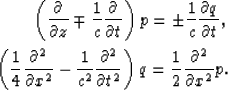Next: Absorbing boundary condition for
Up: Guojian: Absorbing boundary condition
Previous: Introduction
For the one-way wave equation
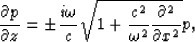
we can write its (2n+1)th order approximation Zhang (1985) in time domain
| 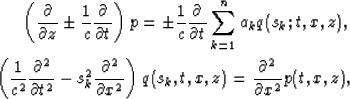 |
(1) |
| (2) |
where q is the auxiliary wavefield, c is the velocity, and
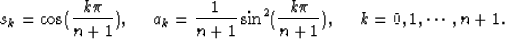
When n=0, we obtain the 5o one-way equation
| 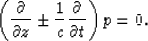 |
(3) |
When n=1, we obtain the 15o one-way equation in Claerbout (1999)
| 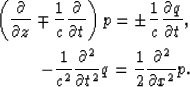 |
(4) |
| (5) |
When n=2, we obtain the 45o one-way wave equation in Claerbout (1999)
| 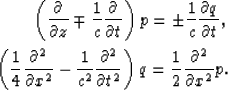 |
(6) |
| (7) |





Next: Absorbing boundary condition for
Up: Guojian: Absorbing boundary condition
Previous: Introduction
Stanford Exploration Project
6/8/2002
![]()
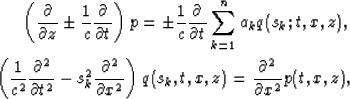
![]()