In the double-porosity formulation,
two distinct phases are assumed to exist at the macroscopic level: (1)
a porous matrix phase with the effective properties K(1),
Km(1), ![]() occupying volume fraction V(1)/V = v(1)
of the total volume and (2)
a macroscopic crack or joint phase occupying the
remaining fraction of the volume V(2)/V = v(2) = 1 - v(1).
In earlier work (Berryman and Pride 2002), methods were developed
to determine the coefficients of this system within a set of
specific modeling assumptions.
But the general laws presented in this section are
independent of all such modeling assumptions, and the analysis to be
presented in later sections is also independent of them as well.
occupying volume fraction V(1)/V = v(1)
of the total volume and (2)
a macroscopic crack or joint phase occupying the
remaining fraction of the volume V(2)/V = v(2) = 1 - v(1).
In earlier work (Berryman and Pride 2002), methods were developed
to determine the coefficients of this system within a set of
specific modeling assumptions.
But the general laws presented in this section are
independent of all such modeling assumptions, and the analysis to be
presented in later sections is also independent of them as well.
The main difference between the single-porosity and double-porosity
formulations is that we allow the average fluid pressure in the
matrix phase to differ from that in the joint phase (thus the term
``double porosity'') over relatively long time scales.
Altogether we have three distinct pressures: confining
(external) pressure ![]() ,pore-fluid pressure
,pore-fluid pressure ![]() , and joint-fluid pressure
, and joint-fluid pressure ![]() .(See Figure dblporpic.)
Treating
.(See Figure dblporpic.)
Treating ![]() and
and ![]() as the independent
variables in the double-porosity theory, we define the dependent variables
to be
as the independent
variables in the double-porosity theory, we define the dependent variables
to be ![]() ,
,![]() ,and
,and
![]() ,which are respectively the total volume dilatation, the
increment of fluid content in the matrix phase, and the increment of
fluid content in the joints. Finally, we assume that the fluid in the matrix
is the same kind of fluid as that in the joints.
,which are respectively the total volume dilatation, the
increment of fluid content in the matrix phase, and the increment of
fluid content in the joints. Finally, we assume that the fluid in the matrix
is the same kind of fluid as that in the joints.
Linear relations among strain, fluid content, and pressure then take the general form
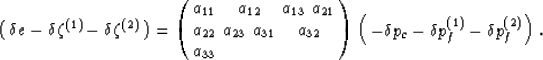 |
(15) |
| |
(16) |
| |
(17) |