In order to implement a fast azimuth moveout operator, we use the PS-DMO operator in the frequency-wavenumber log-stretch domain Rosales (2002); Xu et al. (2001). The f-k log-stretch operator for PS-DMO in 3D takes the form
| |
(8) |
Following Vlad and Biondi's 2001 approach, we construct the PS-AMO operator in this domain. The operator takes the form of
| (9) |
where
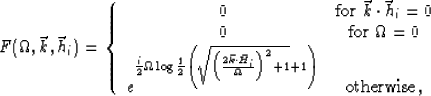 |
(10) |
and ![]() is the spatial frequency vector for the midpoints coordinates
(for this case, the vectors
is the spatial frequency vector for the midpoints coordinates
(for this case, the vectors ![]() and
and ![]() are the same as presented in
the previous section).
are the same as presented in
the previous section).
Rosales (2002) discusses a more accurate PS-DMO operator in this domain.
This new PS-DMO operator distributes the amplitudes correctly along strong dip events.
This operator is just the extension of Zhou et al. (1996) for PS data. Using the improved operator
presented by Rosales (2002) the filter ![]() takes
the form:
takes
the form:
![\begin{displaymath}
F(\Omega,\vec{k},\vec{h}_i) = \left \{ \begin{array}
{cc}
0...
...\right ]} \right \} } & \mbox{otherwise}.
\end{array} \right .\end{displaymath}](img32.gif) |
(11) |